


Next: Restricted PDAGs and Completed
Up: Searching for Bayesian Network
Previous: DAGs and Equivalence Classes
Restricted Acyclic Partially Directed Graphs
The scheme of representation that we will use is slightly different from the formalism of completed PDAGs. It is not necessary for each configuration of our search space (which we call restricted PDAG or RPDAG) to correspond to a different equivalence class; two different RPDAGs may correspond to the same equivalence class. The main reason for this is efficiency: by allowing an equivalence class to be represented (only in some cases) by different RPDAGs, we will gain in efficiency to explore the space. Before explaining this in greater detail, let us define the concept of RPDAG:
As an RPDAG is a PDAG, it could be considered to be a representation of a set of (equivalent) DAGs. We therefore must define which the set of DAGs is represented by a given RPDAG  , i.e. how direction may be given to the links in
, i.e. how direction may be given to the links in  in order to extend it to a DAG. The following definition formalizes this idea.
in order to extend it to a DAG. The following definition formalizes this idea.
We will use 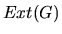 to denote the set of DAGs that are extensions of a given PDAG
to denote the set of DAGs that are extensions of a given PDAG  .
.
Proof:
(a) As  has no directed cycle (condition 2 in Definition 1), then either
has no directed cycle (condition 2 in Definition 1), then either  is already a DAG or it has some links. Let us consider an arbitrary link
is already a DAG or it has some links. Let us consider an arbitrary link  . Using condition 1 in Definition 1, neither
. Using condition 1 in Definition 1, neither  nor
nor  can have a parent. We can then direct the link
can have a parent. We can then direct the link  in either direction without creating an h-h pattern. If we direct the link
in either direction without creating an h-h pattern. If we direct the link  as
as
 and
and  is part of another link
is part of another link  , then we direct it as
, then we direct it as
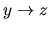 (in order to avoid a new h-h pattern). We can continue directing the links in a chain in this way, and this process cannot generate a directed cycle because, according to condition 3 in Definition 1,
(in order to avoid a new h-h pattern). We can continue directing the links in a chain in this way, and this process cannot generate a directed cycle because, according to condition 3 in Definition 1,  has no completely undirected cycle.
has no completely undirected cycle.
(b) The extension process of  does not modify the skeleton and does not create new h-h patterns. Therefore, all the extensions of
does not modify the skeleton and does not create new h-h patterns. Therefore, all the extensions of  have the same skeleton and the same v-structures (a v-structure is a particular case of h-h pattern), hence they are equivalent.
have the same skeleton and the same v-structures (a v-structure is a particular case of h-h pattern), hence they are equivalent.
It should be noted that condition 4 in Definition 1 is not necessary to prove the results in Proposition 1. This condition is included to ensure that the type of PDAG used to represent subsets of equivalent DAGs is as general as possible. In other words, condition 4 guarantees that an RPDAG is a representation of the greatest number of equivalent DAGs, subject to the restrictions imposed by conditions 1-3 in Definition 1. As we will see in the next proposition, this is achieved by directing the minimum number of edges. For example,
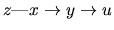 would not be a valid RPDAG. The RPDAG that we would use in this case is
would not be a valid RPDAG. The RPDAG that we would use in this case is
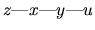 .
.
Proposition 2
Let

be a PDAG verifying the conditions 1-3 in Definition
1. There is then a single RPDAG
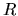
such that
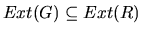
.
Proof:
The proof is constructive. We shall build the RPDAG 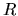 as follows: the skeleton and the h-h patterns of
as follows: the skeleton and the h-h patterns of 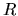 are the same as those in
are the same as those in  . An arc
. An arc
 in
in  shall now be considered such that
shall now be considered such that
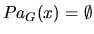 and
and 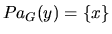 (if such an arc does not exist, then
(if such an arc does not exist, then  itself would be an RPDAG): we convert the arc
itself would be an RPDAG): we convert the arc
 into the link
into the link  . This process is then repeated. Obviously, the PDAG
. This process is then repeated. Obviously, the PDAG 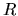 obtained in this way has no directed cycle and verifies condition 4 in Definition 1. Moreover, we cannot obtain a configuration
obtained in this way has no directed cycle and verifies condition 4 in Definition 1. Moreover, we cannot obtain a configuration
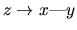 as a subgraph of
as a subgraph of  because
because
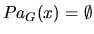 (we only remove the direction of arcs whose initial nodes have no parent). In addition,
(we only remove the direction of arcs whose initial nodes have no parent). In addition,  cannot have any completely undirected cycle because either the arc
cannot have any completely undirected cycle because either the arc
 is not part of any cycle in
is not part of any cycle in  or it is part of a cycle in
or it is part of a cycle in  that must contain at least one h-h pattern (and the directions of the arcs in this pattern will never be removed).
that must contain at least one h-h pattern (and the directions of the arcs in this pattern will never be removed). 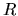 is therefore an RPDAG.
is therefore an RPDAG.
Let us now prove that
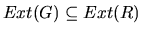 : if
: if 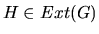 then
then  and
and  have the same skeleton and h-h patterns, hence
have the same skeleton and h-h patterns, hence  and
and 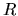 also have the same skeleton and h-h patterns. Moreover, as all the arcs in
also have the same skeleton and h-h patterns. Moreover, as all the arcs in 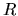 are also arcs in
are also arcs in  , if
, if
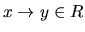 then
then
 , which in turn implies that
, which in turn implies that
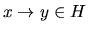 . Therefore, according to Definition 2,
. Therefore, according to Definition 2, 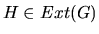 .
.
Finally, let us prove the uniqueness of 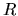 : we already know that any other RPDAG
: we already know that any other RPDAG 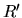 verifying that
verifying that
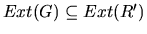 has the same skeleton and h-h patterns as
has the same skeleton and h-h patterns as 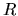 . According to condition 1 in Definition 1, the edges that are not part of any of these h-h patterns but are incident to the middle node
. According to condition 1 in Definition 1, the edges that are not part of any of these h-h patterns but are incident to the middle node  in any h-h pattern
in any h-h pattern
 must be directed away from
must be directed away from  (in order to avoid new h-h patterns). The remaining edges that are not part of any h-h pattern must be undirected, in order to satisfy condition 4 in Definition 1. There is therefore only one RPDAG that matches a given skeleton and a set of h-h patterns, so
(in order to avoid new h-h patterns). The remaining edges that are not part of any h-h pattern must be undirected, in order to satisfy condition 4 in Definition 1. There is therefore only one RPDAG that matches a given skeleton and a set of h-h patterns, so 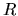 is the only RPDAG verifying that
is the only RPDAG verifying that
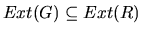 . Figure 6 shows an example of the construction process.
. Figure 6 shows an example of the construction process.
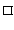
Figure 6:
Illustrating the construction process in Proposition 2: (a) PDAG  ; (b) undirecting the arc
; (b) undirecting the arc
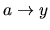 ; (c) undirecting the arc
; (c) undirecting the arc
 ; (d) undirecting the arc
; (d) undirecting the arc
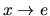 , thus obtaining the RPDAG
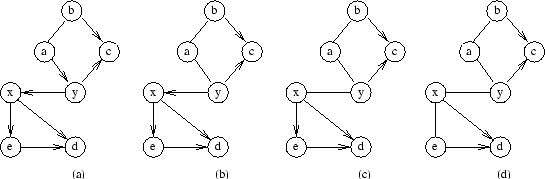
, thus obtaining the RPDAG 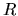
 |
The following proposition ensures that the concept of RPDAG allows us to define a partition in the space of DAGs.
Proof:
Let  be any DAG. Then
be any DAG. Then  itself is a PDAG and obviously
itself is a PDAG and obviously 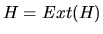 . By applying the result in Proposition 2, we can assert that there is a single RPDAG
. By applying the result in Proposition 2, we can assert that there is a single RPDAG  such that
such that
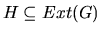 .
.
In the proposition below, we show the properties which are common to all the DAGs belonging to the same extension of an RPDAG.
Proposition 4
Two DAGs belong to the extension of the same RPDAG if and only if they have the same skeleton and the same h-h patterns.
Proof:
The necessary condition is obvious. Let us prove the sufficient condition: let  and
and 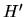 be two DAGs with common skeleton and h-h patterns. We shall construct a PDAG
be two DAGs with common skeleton and h-h patterns. We shall construct a PDAG  as follows: the skeleton and the h-h patterns of
as follows: the skeleton and the h-h patterns of  are the same as those in
are the same as those in  and
and 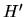 ; the edges that have the same orientation in
; the edges that have the same orientation in  and
and 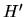 are directed in
are directed in  in the same way; the other edges in
in the same way; the other edges in  remain undirected. From Definition 2, it is clear that
remain undirected. From Definition 2, it is clear that
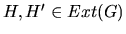 .
.
 has no directed cycles because
has no directed cycles because  and
and 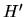 are DAGs.
are DAGs.  has no completely undirected cycles, since all the cycles in
has no completely undirected cycles, since all the cycles in  and
and 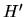 share at least the h-h patterns. In addition,
share at least the h-h patterns. In addition,
 cannot be a subgraph of
cannot be a subgraph of  because this would imply the existence of the subgraphs
because this would imply the existence of the subgraphs
 and
and
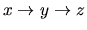 in
in  and
and 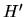 , respectively, and therefore these two DAGs would not have the same h-h patterns.
, respectively, and therefore these two DAGs would not have the same h-h patterns.
Therefore, the PDAG  satisfies conditions 1-3 in Definition 1. By applying Proposition 2, we can then build a single RPDAG
satisfies conditions 1-3 in Definition 1. By applying Proposition 2, we can then build a single RPDAG 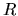 such that
such that
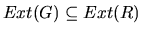 , hence
, hence
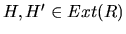 .
.
A characterization of the extension of an RPDAG that will be useful later is:
Proof:
 Necessary condition:
Necessary condition:
-
 : Let
: Let  , i.e.,
, i.e.,
 . Then, from condition 2 in Definition 2,
. Then, from condition 2 in Definition 2,
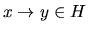 , i.e.,
, i.e., 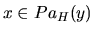 . Moreover,
. Moreover,
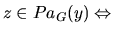
 is an h-h pattern in
is an h-h pattern in  . From condition 3 in Definition 2, this occurs if and only if
. From condition 3 in Definition 2, this occurs if and only if
 is an h-h pattern in
is an h-h pattern in  , which is equivalent to
, which is equivalent to 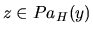 . Therefore,
. Therefore,
 .
.
-
 and
and
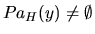 : Let
: Let 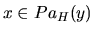 . If there is another node
. If there is another node 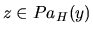 , then
, then
 is an h-h pattern in
is an h-h pattern in  and therefore it is also an h-h pattern in
and therefore it is also an h-h pattern in  , which contradicts the fact that
, which contradicts the fact that
 . So,
. So,  cannot have more than one parent in
cannot have more than one parent in  , hence
, hence 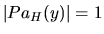 .
.
 Sufficient condition:
Sufficient condition:
- If
 then
then
 . From condition 2 we have
. From condition 2 we have
 , hence
, hence
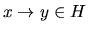 .
.
- If
 is an h-h pattern in
is an h-h pattern in  , once again from condition 2,
, once again from condition 2,
 and therefore
and therefore
 is an h-h pattern in
is an h-h pattern in  .
.
- If
 is an h-h pattern in
is an h-h pattern in  , then
, then
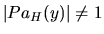 and
and
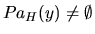 . So, from condition 3, we obtain
. So, from condition 3, we obtain
 and, from condition 2,
and, from condition 2,
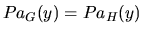 . Therefore
. Therefore
 is an h-h pattern in
is an h-h pattern in  .
.
Subsections



Next: Restricted PDAGs and Completed
Up: Searching for Bayesian Network
Previous: DAGs and Equivalence Classes
Luis Miguel de Campos Ibáñez
2003-05-30
 ,
,
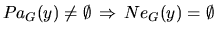 .
.
 does not contain any directed cycle.
does not contain any directed cycle.
 does not contain any completely undirected cycle, i.e. a cycle containing only links.
does not contain any completely undirected cycle, i.e. a cycle containing only links.
 exists in
exists in  then either
then either
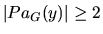 or
or
 .
.
 exists in
exists in  only if it is either part of an h-h pattern or there is another arc (originated by an h-h pattern) going to
only if it is either part of an h-h pattern or there is another arc (originated by an h-h pattern) going to  .
.
