Restricted PDAGs and Completed PDAGs

Let us now examine the main differences between the different representations: a representation based on PDAGs ensures that every equivalence class has a unique representation, but there are PDAGs that do not correspond to any equivalence class (in other words, the mapping from equivalence classes to PDAGs is injective). On the other hand, our representation based on RPDAGs guarantees that every RPDAG corresponds to an equivalence class (proposition 1) but does not ensure that every equivalence class has a single representation (the mapping from equivalence classes to RPDAGs is onto). However, the mapping from equivalence classes to CPDAGs is bijective. Figures 7.a, 7.b and 7.c show the three RPDAGs corresponding to the same equivalence class; the associated completed PDAG is shown in Figure 7.d. In this example, the number of DAGs in the equivalence class is 12.

Figure 7: (a), (b) and (c) Three RPDAGs corresponding to the same equivalence class; (d) the associated completed PDAG

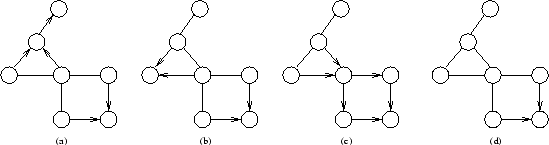
As we can see, the difference appears when there are triangular structures. If we compare the definition of RPDAG (Definition 1) with the characterization of CPDAGs (Theorem 2), we may observe that the essential difference is that a CPDAG may have completely undirected cycles, but these cycles must be chordal. In RPDAGs, undirected cycles are therefore forbidden, whereas in CPDAGs undirected non-chordal cycles are forbidden.

It should be noted that we could also define RPDAGs by replacing condition 3 in Definition 1 for its equivalent: The subgraph induced by every chain component of $G$ is a tree (which is a specific type of chordal graph). In this way, the similarities and differences between CPDAGs and RPDAGs are even clearer. Any of the RPDAGs in the same equivalence class is obtained from the corresponding CPDAG by removing some of the links (converting them into arcs) in order to obtain a tree structure.

Examining the problem from another perspective, from Theorem 1 and Proposition 4 we can see that the role played by the v-structures in CPDAGs is the same as that played by the h-h patterns in RPDAGs.

It is also interesting to note that the number of DAGs which are extensions of a given RPDAG, $G$, can be calculated very easily: the subgraph induced by each chain component of $G$ is a tree, and this tree can be directed in different ways by selecting any of the nodes as the root node. Moreover, we can proceed independently within each chain component. The number of DAGs in $Ext(G)$ is therefore equal to the product of the number of nodes within each chain component of $G$. Regarding the number of RPDAGs that represent the same equivalence class, this number grows exponentially with the size of the undirected cliques in the CPDAG. For example, if the subgraph induced by a chain component in a CPDAG consists of a complete subgraph of $m$ nodes, then the number of RPDAG representations is $\frac{m!}{2}$. This obviously does not mean that a search method based on RPDAGs must explore all these equivalent representations.

Our reason for using RPDAGs is almost exclusively practical. In fact, RPDAGs do not have a clear semantics (they are a somewhat hybrid creature, between DAGs and completed PDAGs). We can only say that RPDAGs would correspond to sets of equivalent DAGs which share all the causal patterns where an effect node has at least two causes (and only the causal patterns where a single cause provokes an effect are not determined). This is not problematic when we are performing model selection but it becomes critical if we are doing model averaging: without a semantic understanding of the class of RPDAGs, it will be quite difficult to assign a prior to them.

Our intention is to trade the uniqueness of the representation of equivalence classes of DAGs (CPDAGs) for a more manageable one (RPDAGs): testing whether a given PDAG $G$ is an RPDAG is easier than testing whether $G$ is a completed PDAG. In the first case, the consistency check involves testing for the absence of directed and completely undirected cycles (the complexity of these tests and those necessary to verify whether a directed graph is a DAG is exactly the same), whereas in the second case, in addition to testing for the absence of directed and partially directed cycles, we also need to perform chordality tests and check that each arc is part of one of the induced subgraphs displayed in Figure 2. The price we have to pay for using RPDAGs is that we may occasionally need to evaluate an equivalence class more than once. In the next section, we will examine how a local search method which uses RPDAGs can also take advantage of the decomposability property of a scoring function in order to efficiently evaluate neighboring structures.