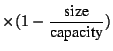Preliminary concepts

The most primitive constructs in a compositional modeller are participants, relations and assumptions. This subsection summarises these concepts and explains how they are represented herein.

Participants² refer to the objects of interest, which are involved in the scenario or its model. These participants may be real-world objects or conceptual objects, such as variables that express features of real-world objects in a mathematical model. For instance, a population of a species is a typical example of a real-world object, and a variable that expresses the number of individuals of this species forms an example of a conceptual object. It is natural to group objects that share something in common into classes. Participants are herein grouped into participant classes, with each representing a set of participants that share certain common features. Each class will be given a name for easy reference.

Relations describe how the participants are related to one another. As with participants, some relations represent a real-world relationship, such as:

predation(frog, insect) (1)

Other relations may be conceptual in nature, such as equation (2), which describes an important textbook model of logistic population growth [11]:

$$\frac{d}{dt} = \times \times(1-\frac{\text{size}}{\text{capacity}})$$ (2)

To be consistent with other compositional modelling approaches, this paper employs a LISP-style notation for relations. As such, the above two sample relations become:

$$\texttt{(predation frog insect)}$$ (1)

$$\texttt{(d/dt change (* change-rate size (- 1 (/ size capacity))))}$$ (2)

Assumptions form a special type of relation that are employed to distinguish between alternative model design decisions. Internally, assumptions will be stored in the form of assumption nodes in the ATMS (see section 3.3.1), but in the knowledge base, assumptions appear as relations with a specific syntax and semantics.

Two types of assumptions are employed in this article. Relevance assumptions state what phenomena are to be included in or excluded from the scenario model. Typical examples of phenomena are the population growth and predation phenomena. The general format of a relevance assumption is shown in (3). The phenomenon that is incorporated in the scenario model when describing a relevance assumption is identified by $\langle$name$\rangle$ and is specific to the subsequent participants or relations. For example, relevance assumption (4) states that the growth of participant ?population is to be included in the model.

$$\texttt{(relevant}\quad\langle\textit{name}\rangle\quad[\{\langle\textit{participant}\rangle\}\mid\langle\textit{relation}\rangle]\texttt{)}$$ (3)

$$\texttt{(relevant growth ?population)}$$ (4)

Model assumptions specify which type of model is utilised to describe the behaviour of a certain participant or relation. Typical examples of model types include the exponential [26] and the logistic [43] model types of population growth. The formal specification of a model assumption is given in (5). Often the $\langle$name$\rangle$ in (5) corresponds to the name of a known (partial) model of the phenomenon or process being described. The example in (6) states that the population ?population is being modelled using the logistic approach.

$$\texttt{(model}\quad[\langle\textit{participant}\rangle\mid\langle\textit{relation}\rangle]\quad\langle\textit{name}\rangle\texttt{)}$$ (5)

$$\texttt{(model ?population logistic)}$$ (6)