- ... produced1
- Here, the
arguments are under the form of an ``Explanation-Conclusion
Pair''. This is one possible way to compute arguments. See
also [17,25,20,22,23,12,15,2].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline2845#2
- Weights being probabilities, the weight of an
argument is the probability of the conjunction of the formulae of
the argument, and the weight of
 is the probability of the
disjunction of
is the probability of the
disjunction of  and
and  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... etc.3
- Here, we
consider only the interactions corresponding to attacks between
arguments. There exist also some other types of interactions (for
example, arguments which reinforce other arguments instead of
attacking them, see [14,24]). For this kind of
interaction, graduality has not been considered.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... arguments4
- Here, the initial knowledge base is useless.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... arguments5
- For example, using [4]'s
valuation, we can decide that all the arguments whose value is
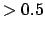 are selected, because
are selected, because 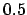 is the mean value of the set of
values; Another possibility, with different valuations
(interaction-based or intrinsic), is to accept an argument when its
value is better than the value of each of its attackers.
is the mean value of the set of
values; Another possibility, with different valuations
(interaction-based or intrinsic), is to accept an argument when its
value is better than the value of each of its attackers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline2921#6
-
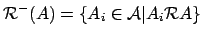 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline2927#7
-
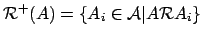 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... root8
- The word ``root'' is used in an informal
sense (it just means that there are in the graph some paths
leading to this node). This term and other terms (leaf, branch,
path, ...) which are used in this document are standard in
graph theory but may have a different definition. They are usual
terms in the argumentation domain. Please see
Definition 1 in order to know their precise meaning
in this document. These definitions simply take into account the
fact that the directed edges of our graph link attackers to
attacked argument).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... attackers9
 is a leaf iff
is a leaf iff
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... path10
- We will assume that there
exists an infinity of such paths. This assumption greatly
simplifies the handling of leaves later in the paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...cycle11
- This
definition of a cycle corresponds to the definition of an
elementary cycle in graph theory (an elementary cycle does not
contain 2 edges with the same initial extremity, or the same
ending extremity).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
equivalent12
- In [9]'s work, direct attackers (resp.
defenders) are also indirect attackers (resp. defenders) which is
not true in our definitions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
arguments13
- We pursue a work initiated in [7] and
propose some improvements.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ratio14
- The golden ratio is a famous
number since the antiquity which has several interesting properties
in several domains (architecture, for example).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complete15
- A complete preordering on
 means that any
two elements of
means that any
two elements of  are comparable.
are comparable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
arguments16
-
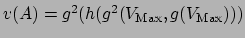 and
and
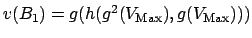 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline3641#17
- Otherwise it is false :
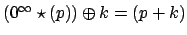 ,
whereas
,
whereas
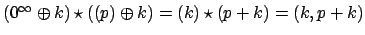 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tuples18
- This
definition is different from the definition given in [7].
The ideas are the same but the formalisation is different.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
both19
- The proof is the following:.
- If
 is not a leaf, at least one of the tuples is not empty,
because there exists at least one branch whose length is
is not a leaf, at least one of the tuples is not empty,
because there exists at least one branch whose length is 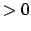 leading to
leading to  (see Definitions 8
and 10).
(see Definitions 8
and 10).
- And, if
 is a leaf, there also exists at least one defence
branch because the path from
is a leaf, there also exists at least one defence
branch because the path from  to
to  is allowed and its length is
is allowed and its length is
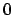 (in fact, there are an infinity of such paths - see
Definition 1) and no attack branch leading to the leaf
(see Definition 10).
(in fact, there are an infinity of such paths - see
Definition 1) and no attack branch leading to the leaf
(see Definition 10).
So, the value of a leaf is
![$[0^{\infty},()]$](img257.png) , and it is impossible
that
, and it is impossible
that
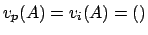 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exists20
- The
operator mod is the modulo function.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tuple21
- The proof is the following:.
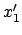 contains only even integers.
contains only even integers.
- For each k,
 since
since 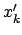 is the result of the
addition of a tuple and an integer.
is the result of the
addition of a tuple and an integer.
- If
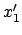 is not empty, let
is not empty, let 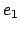 denote the least even integer
present in
denote the least even integer
present in 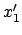 . As
. As
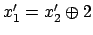 ,
, 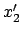 is not empty and
is not empty and
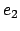 will denote the least integer present in
will denote the least integer present in 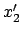 . We have
. We have 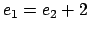 . So, we are able to build a sequence of positive even integers
. So, we are able to build a sequence of positive even integers
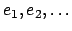 , which is strictly decreasing. That is impossible. So,
, which is strictly decreasing. That is impossible. So, 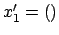 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline4481#22
- We will also use the notation
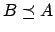 defined by:
defined by:
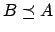 iff
iff  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... than23
- With
the valuation proposed in [4], we obtain:
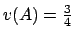 and
and
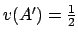 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... acceptability24
- This work has been
presented in a workshop [6].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cases25
- The terminology
used in this section is also used in the domain of nonmonotonic
reasoning, see [19]: the word uni comes from the word
universal which is a ``synonym'' of the word skeptical, and the word exi comes from the word existential which is a ``synonym'' of the word credulous. We have chosen to use the words uni and exi because they recall the logical quantificators
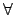 (for all) and
(for all) and 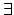 (exists at least one).
(exists at least one).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... coincide26
- If there is only one
extension then the fact that
 belongs to all the extensions is
equivalent to the fact that
belongs to all the extensions is
equivalent to the fact that  belongs to at least one extension.
Moreover, with only one extension containing
belongs to at least one extension.
Moreover, with only one extension containing  , all the attackers
of
, all the attackers
of  do not belong to an extension. So,
do not belong to an extension. So,  is cleanly-accepted.
is cleanly-accepted.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stable27
- This corresponds to the
consistent argumentation system proposed by [9].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... attackers28
- This idea is also used in
the notion of ``defeat'' proposed by [3]. So, there is a
link between a ``well-defended argument'' and an argument which is
not ``attacked'' in the sense of [3] by its direct
attackers. Note that, in [3], the valuation is an extra
knowledge added in the argumentation framework. In contrast, here,
the
 -preference is extracted from the attack graph.
-preference is extracted from the attack graph.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cycles29
- So,
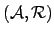 is well-founded.
is well-founded.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
identical''30
- Proof: let
 be a non-increasing function, let
be a non-increasing function, let 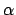 and
and 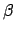 be two fixpoints of
be two fixpoints of
 . If
. If
 , we may suppose that
, we may suppose that
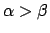 , so
, so
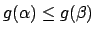 (since
(since  is non-increasing), so
is non-increasing), so
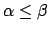 (since
(since 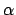 and
and 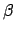 are fixpoints of
are fixpoints of  ), which is in
contradiction with the assumption
), which is in
contradiction with the assumption
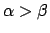 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... case31
- We work case by case in order to avoid the complex
cases in which we have several simultaneous simple
modifications. For example, the modification of the length of a
branch which
changes the status of the branch (an even integer replaced by an odd
integer) is a complex case corresponding to two simple cases: the
removal of a branch with a given status, then the addition of a new
branch with a different status.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline5979#32
-
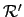 is the
restriction of
is the
restriction of 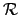 to
to
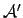 if and only if
if and only if
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 is not a leaf, at least one of the tuples is not empty,
because there exists at least one branch whose length is
is not a leaf, at least one of the tuples is not empty,
because there exists at least one branch whose length is 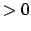 leading to
leading to  (see Definitions 8
and 10).
(see Definitions 8
and 10).
 is a leaf, there also exists at least one defence
branch because the path from
is a leaf, there also exists at least one defence
branch because the path from  to
to  is allowed and its length is
is allowed and its length is
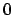 (in fact, there are an infinity of such paths - see
Definition 1) and no attack branch leading to the leaf
(see Definition 10).
(in fact, there are an infinity of such paths - see
Definition 1) and no attack branch leading to the leaf
(see Definition 10).
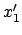 contains only even integers.
contains only even integers.
 since
since 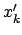 is the result of the
addition of a tuple and an integer.
is the result of the
addition of a tuple and an integer.
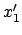 is not empty, let
is not empty, let 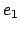 denote the least even integer
present in
denote the least even integer
present in 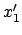 . As
. As
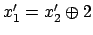 ,
, 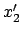 is not empty and
is not empty and
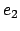 will denote the least integer present in
will denote the least integer present in 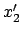 . We have
. We have 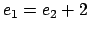 . So, we are able to build a sequence of positive even integers
. So, we are able to build a sequence of positive even integers
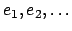 , which is strictly decreasing. That is impossible. So,
, which is strictly decreasing. That is impossible. So, 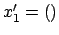 .
.