A Concrete Example

Our experiments have so far focused on artificial problems and have aimed at characterising the strengths and weaknesses of the various approaches. We now look at a concrete example in order to give a sense of the size of more interesting problems that these techniques can solve. Our example is derived from the Miconic elevator classical planning benchmark [35]. An elevator must get a number of passengers from their origin floor to their destination. Initially, the elevator is at some arbitrary floor and no passenger is served nor has boarded the elevator. In our version of the problem, there is one single action which causes the elevator to service a given floor, with the effect that the unserved passengers whose origin is the serviced floor board the elevator, while the boarded passengers whose destination is the serviced floor unboard and become served. The task is to plan the elevator movement so that all passengers are eventually served.¹⁴ There are two variants of Miconic. In the `simple' variant, a reward is received each time a passenger becomes served. In the `hard' variant, the elevator also attempts to provide a range of priority services to passengers with special requirements: many passengers will prefer travelling in a single direction (either up or down) to their destination, certain passengers might be offered non-stop travel to their destination, and finally, passengers with disabilities or young children should be supervised inside the elevator by some other passenger (the supervisor) assigned to them. Here we omit the VIP and conflicting group services present in the original hard Miconic problem, as the reward formulae for those do not create additional difficulties. Our formulation of the problem makes use of the same propositions as the PDDL description of Miconic used in the 2000 International Planning Competition: dynamic propositions record the floor the elevator is currently at and whether passengers are served or boarded, and static propositions record the origin and destination floors of passengers, as well as the categories (non-stop, direct-travel, supervisor, supervised) the passengers fall in. However, our formulation differs from the PDDL description in two interesting ways. Firstly, since we use rewards instead of goals, we are able to find a preferred solution even when all goals cannot simultaneously be satisfied. Secondly, because priority services are naturally described in terms of non-Markovian rewards, we are able to use the same action description for both the simple and hard versions, whereas the PDDL description of hard miconic requires additional actions (up, down) and complex preconditions to monitor the satisfaction of priority service constraints. The reward schemes for Miconic can be encapsulated through four different types of reward formula.

1. In the simple variant, a reward is received the first time each passenger 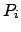$P_i$ is served:

   PLTL:	$ServedP_i \wedge \circleddash \boxminus \neg ServedP_i$
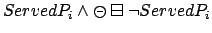   $FLTL:	$\neg ServedP_i \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(ServedP_i \wedge \mbox{\$})$

2. Next, a reward is received each time a non-stop passenger 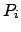$P_i$ is served in one step after boarding the elevator:

   PLTL:	$NonStopP_i \wedge \circleddash \circleddash \neg BoardedP_i \wedge \circleddash \circleddash \neg ServedP_i \wedge ServedP_i$
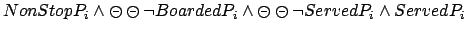   $FLTL:	$\mbox{$\Box$}((NonStopP_i \wedge \neg BoardedP_i \wedge \neg ServedP_i \wedge \... ...mm}{$\scriptstyle \bigcirc$}\raisebox{0.6mm}{$\scriptstyle \bigcirc$}\mbox{\$})$

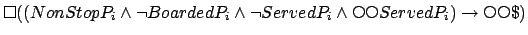3. Then, a reward is received each time a supervised passenger 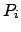$P_i$ is served while having been accompanied at all times inside the elevator by his supervisor¹⁵ 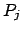$P_j$:

   PLTL:	$SupervisedP_i \wedge SupervisorP_jP_i \wedge ServedP_i \wedge$
   	$\circleddash \boxminus \neg ServedP_i \wedge \boxminus (BoardedP_i \rightarrow BoardedP_j)$

    
   

   $FLTL:	$\neg ServedP_i \makebox[1em]{$\mathbin{\mbox{\sf U}}$}$		$((BoardedP_i \wedge SupervisedP_i \wedge \neg(BoardedP_j \wedge SupervisorP_jP_i) \wedge$
   			$~\neg ServedP_i) \vee (ServededP_i \wedge \mbox{\$}))$

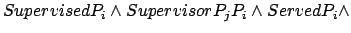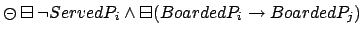4. Finally, reward is received each time a direct travel passenger 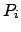$P_i$ is served while having travelled only in one direction since boarding, e.g., in the case of going up:

   PLTL:	$DirectP_i \wedge ServedP_i \wedge \circleddash \neg ServedP_i \wedge$
   	$((\bigvee_j \bigvee_{k > j} (AtFloor_k \wedge \circleddash AtFloor_j))\mathbin{\mbox{\sf S}} (BoardedP_i \wedge \circleddash \neg BoardedP_i))$

    
   

   $FLTL:	$\mbox{$\Box$}((DirectP_i \wedge BoardedP_i) \rightarrow (\neg ServedP_i \makebox[1em]{$\mathbin{\mbox{\sf U}}$}$		$((\neg (\bigvee_j \bigvee_{k > i} AtFloor_j \wedge \raisebox{0.6mm}{$\scriptstyle \bigcirc$}AtFloor_k) \wedge$
   			$~\neg ServedP_i) \vee (servedP_i \wedge \mbox{\$}))))$

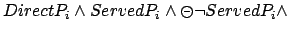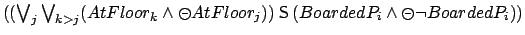   and similarly in the case of going down.

Experiments in this section were run on a Dual Pentium4 3.4GHz GNU/Linux 2.6.11 machine with 1GB of ram. We first experimented with the simple variant, giving a reward of 50 each time a passenger is first served. Figure 19 shows the CPU time taken by the various approaches to solve random problems with an increasing number $n$ of floors and passengers, and Figure 20 shows the number of states expanded when doing so. Each data point corresponds to just one random problem. To be fair with the structured approach, we ran PLTLSTR(A) which is able to exploit reachability from the start state. A first observation is that although PLTLSTR(A) does best for small values of $n$, it quickly runs out of memory. 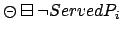PLTLSTR(A) and PLTLSIM both need to track formulae of the form $\circleddash \boxminus \neg ServedP_i$ while PLTLSIM does not, and we conjecture that this is why they run out of memory earlier. A second observation is that attempts at PLTL minimisation do not pay very much here. While PLTLMIN has reduced memory because it tracks fewer subformulae, the size of the MDP it produces is identical to the size of the PLTLSIM MDP and larger than that of the FLTL MDP. This size increase is due to the fact that PLTL approaches label differently e-states in which the same passengers are served, depending on who has just become served (for those passengers, the reward formula is true at the e-state). In contrast, our FLTL implementation with progression one step ahead labels all these e-states with the reward formulae relevant to the passengers that still need to be served, the other formulae having progressed to $\top$. The gain in number of expanded states materialises into run time gains, resulting in FLTL eventually taking the lead.

Figure 19: Simple Miconic - Run Time

Figure 20: Simple Miconic - Number of Expanded States

Figure 21: Effect of a Simple Heuristic on Run Time

Figure 22: Effect of a Simple Heuristic on the Number of Expanded States

Figure 23: Hard Miconic - Run Time

Figure 24: Hard Miconic - Number of Expanded States

Our second experiment illustrates the benefits of using an even extremely simple admissible heuristic in conjunction with FLTL. Our heuristic is applicable to discounted stochastic shortest path problems, and discounts rewards by the shortest time in the future in which they are possible. Here it simply amounts to assigning a fringe state to a value of 50 times the number of still unserved passengers (discounted once), and results in avoiding floors at which no passenger is waiting and which are not the destination of a boarded passenger. Figures 21 and 22 compare the run time and number of states expanded by FLTL when used in conjunction with value iteration (valIt) to when it is used in conjunction with an LAO* search informed by the above heuristic (LAO(h)). Uninformed LAO* (LAO*(u), i.e. LAO* with a heuristic of $50*n$ at each node) is also included as a reference point to show the overhead induced by heuristic search. As can be seen from the graphs, the heuristic search generates significantly fewer states and this eventually pays in terms of run time. In our final experiment, we considered the hard variant, giving a reward of 50 as before for service (1), a reward of 2 for non-stop travel (2), a reward of 5 for appropriate supervision (3), and a reward of 10 for direct travel (2). Regardless of the number $n$ of floors and passengers, problems only feature a single non-stop traveller, a third of passengers require supervision, and only half the passengers care about traveling direct. CPU time and number of states expanded are shown in Figures 23 and 24, respectively. As in the simple case, PLTLSIM and PLTLSTR quickly run out of memory. Formulae of type (2) and (3) create too many additional variables to track for these approaches, and the problem does not seem to exhibit enough structure to help PLTLSTR. FLTL remains the fastest. Here, this does not seem to be so much due to the size of the generated MDP which is just slightly below that of the PLTLMIN MDP, but rather to the overhead incurred by minimisation. Another observation arising from this experiment is that only very small instances can be handled in comparison to the classical planning version of the problem solved by state of the art optimal classical planners. For example, at the 2000 International Planning Competition, the PROPPLAN planner [24] optimally solved instances of hard Miconic with 20 passengers and 40 floors in about 1000 seconds on a much less powerful machine.