- ... that:1
- Technically, the definition allows the sets of actions
 and
and  to be different, but any action in which they differ must be
inapplicable in reachable states in the NMRDP and in all e-states in
the equivalent MDP. For all practical purposes,
to be different, but any action in which they differ must be
inapplicable in reachable states in the NMRDP and in all e-states in
the equivalent MDP. For all practical purposes,  and
and  can be seen as
identical.
can be seen as
identical.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... in2
- The size
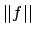 of
a reward formula is measured as its length and the size
of
a reward formula is measured as its length and the size  of
a set of reward formulae
of
a set of reward formulae  is measured as the sum of the lengths of
the formulae in
is measured as the sum of the lengths of
the formulae in  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...3
-
If there is no
 such that
such that
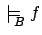 , which is the case for
any $-free
, which is the case for
any $-free  which is not a logical theorem, then
which is not a logical theorem, then  is
is
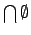 - i.e.
- i.e.  following normal set-theoretic
conventions. This limiting case does no harm, since $-free
formulae do not describe the attribution of rewards.
following normal set-theoretic
conventions. This limiting case does no harm, since $-free
formulae do not describe the attribution of rewards.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...4
- It is an open question whether the set of representable
behaviours is the same for $FLTL as for PLTL, that is
star-free regular languages. Even if the
behaviours were the same, there is little hope that a practical
translation from one to the other exists.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...5
- These difficulties are inherent in the use of linear-time
formalisms in contexts where the principle of directionality must be
enforced. They are shared for instance by formalisms developed for
reasoning about actions such as the Event Calculus and LTL action
theories, see e.g., [13].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... set6
- Strictly speaking, a multiset, but for convenience we
represent it as a set, with the rewards for multiple occurrences of
the same formula in the multiset summed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reward-normal7
- We extend the definition of reward-normality to reward
specification functions in the obvious way, by requiring that all
reward formulae involved be reward normal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...8
- Care is needed over the notion of `semantic equivalence'.
Because rewards are additive, determining equivalence may involve
arithmetic as well as theorem proving. For example, the reward
function specification
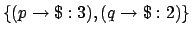 is equivalent to
is equivalent to
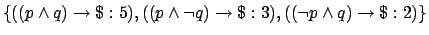 although there is no one-one correspondence between
the formulae in the two sets.
although there is no one-one correspondence between
the formulae in the two sets.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... methods.9
- It would be interesting, on the
other hand, to use PLTLSTR in conjunction with symbolic versions
of such methods, e.g. Symbolic LAO* [21] or Symbolic
RTDP [22].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... previously:10
- Here is an
executive summary of the answers for the executive reader. 1. no,
2. yes, 3. yes, 4. PLTLSTR and FLTL, 5. PLTLSIM, 6. yes,
7. yes and no, respectively, 8. yes, 9. no and yes, respectively.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... properties11
-
 in $FLTL
in $FLTL
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
side.12
- The figures are not necessarily valid for
non-completely connected NMRDPs. Unfortunately, even for completely
connected domains, there does not appear to be a much cheaper way to
determine the MDP size than to generate it and count states.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
unreachable:13
- Here we sometimes speak of conditions and goals
being `reachable' or `achievable' rather than `feasible', although
they may be temporally extended. This is to keep in line with
conventional vocabulary as in the phrase `reachability analysis'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
served.14
- We have experimented with stochastic variants of
Miconic where passengers have some small probability of desembarking
at the wrong floor. However, we find it more useful to present
results for the deterministic version since it is closer to the
Miconic deterministic planning benchmark and since, as we have shown
before, rewards have a far more crucial impact than dynamics on the
relative performance of the methods.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... supervisor15
- To understand the $FLTL formula,
observe that we get a reward iff
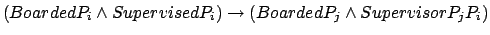 holds until
holds until  becomes true, and recall that the formula
becomes true, and recall that the formula
![$\neg q \makebox[1em]{$\mathbin{\mbox{\sf U}}$}((\neg p
\wedge \neg q) \vee (q \wedge \mbox{\$}))$](img433.png) rewards the holding of
rewards the holding of  until the occurrence of
until the occurrence of  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
time,16
- On each given problem, planners had 15mn to run whatever
computation they saw as appropriate (including parsing,
pre-processing, and policy generation if any), and execute 30 trial
runs of the generated policy from an initial state to a goal state.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... strategy.17
- More
sophisticated near-optimal strategies for deterministic blocks world
exist (see [42]), but are much more complex to
encode and might have caused time performance problems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... probabilities.18
- We would
not argue, on the other hand, that CTL is necessary for
representing non-Markovian rewards.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... goal19
- Where
 is an atemporal formula,
GOALP(
is an atemporal formula,
GOALP( ) is true iff
) is true iff  is true of all goal states.
is true of all goal states.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conducted20
- None of those are included in this paper,
however.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.