Language and Semantics
Compactly representing non-Markovian reward functions reduces to
compactly representing the behaviours of interest, where by
behaviour we mean a set of finite sequences of states (a subset
of  ), e.g. the
), e.g. the
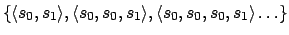 in
Figure 1. Recall that the reward is issued at the end
of any prefix
in
Figure 1. Recall that the reward is issued at the end
of any prefix  in that set. Once behaviours are compactly
represented, it is straightforward to represent non-Markovian reward
functions as mappings from behaviours to real numbers - we shall
defer looking at this until Section 3.6.
To represent behaviours compactly, we adopt a version of future linear
temporal logic (FLTL) (see [20]), augmented with a
propositional constant `$', intended to be read `The behaviour
we want to reward has just happened' or `The reward is received
now'. The language $FLTL begins with a set of basic propositions
in that set. Once behaviours are compactly
represented, it is straightforward to represent non-Markovian reward
functions as mappings from behaviours to real numbers - we shall
defer looking at this until Section 3.6.
To represent behaviours compactly, we adopt a version of future linear
temporal logic (FLTL) (see [20]), augmented with a
propositional constant `$', intended to be read `The behaviour
we want to reward has just happened' or `The reward is received
now'. The language $FLTL begins with a set of basic propositions
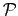 giving rise to literals:
giving rise to literals:
where  and
and  stand for `true' and `false', respectively.
The connectives are classical
stand for `true' and `false', respectively.
The connectives are classical 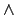 and
and 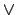 , and the temporal
modalities
, and the temporal
modalities
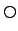 (next) and
(next) and
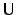 (weak until), giving
formulae:
(weak until), giving
formulae:
Our `until' is weak:
![$f_1 \makebox[1em]{$\mathbin{\mbox{\sf U}}$}f_2$](img200.png) means
means 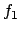 will be true from
now on until
will be true from
now on until 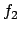 is, if ever. Unlike the more commonly used strong
`until', this does not imply that
is, if ever. Unlike the more commonly used strong
`until', this does not imply that  will eventually be true. It
allows us to define the useful operator
will eventually be true. It
allows us to define the useful operator  (always):
(always):
![$\mbox{$\Box$}f
\equiv f \makebox[1em]{$\mathbin{\mbox{\sf U}}$}\mbox{$\bot$}$](img204.png) (
( will always be true from now on). We also
adopt the notations
will always be true from now on). We also
adopt the notations
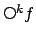 for
for  iterations of the
iterations of the
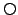 modality (f will be true in exactly
modality (f will be true in exactly  steps),
steps),
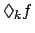 for
for
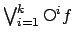 (f will be true within the next
(f will be true within the next  steps), and
steps), and
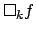 for
for
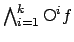 (
( will be true throughout the next
will be true throughout the next  steps).
Although negation officially occurs only in literals, i.e., the
formulae are in negation normal form (NNF), we allow ourselves to
write formulae involving it in the usual way, provided that they have
an equivalent in NNF. Not every formula has such an equivalent,
because there is no such literal as
steps).
Although negation officially occurs only in literals, i.e., the
formulae are in negation normal form (NNF), we allow ourselves to
write formulae involving it in the usual way, provided that they have
an equivalent in NNF. Not every formula has such an equivalent,
because there is no such literal as 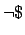 and because
eventualities (`f will be true some time') are not expressible. These
restrictions are deliberate. If we were to use our notation and logic
to theorise about the allocation of rewards, we would indeed
need the means to say when rewards are not received or to express
features such as liveness (`always, there will be a reward
eventually'), but in fact we are using them only as a mechanism for
ensuring that rewards are given where they should be, and for this
restricted purpose eventualities and the negated dollar are not
needed. In fact, including them would create technical difficulties in
relating formulae to the behaviours they represent.
The semantics of this language is similar to that of FLTL, with an
important difference: because the interpretation of the constant
and because
eventualities (`f will be true some time') are not expressible. These
restrictions are deliberate. If we were to use our notation and logic
to theorise about the allocation of rewards, we would indeed
need the means to say when rewards are not received or to express
features such as liveness (`always, there will be a reward
eventually'), but in fact we are using them only as a mechanism for
ensuring that rewards are given where they should be, and for this
restricted purpose eventualities and the negated dollar are not
needed. In fact, including them would create technical difficulties in
relating formulae to the behaviours they represent.
The semantics of this language is similar to that of FLTL, with an
important difference: because the interpretation of the constant
 depends on the behaviour
depends on the behaviour  we want to reward (whatever
that is), the modelling relation
we want to reward (whatever
that is), the modelling relation  must be indexed by
must be indexed by  . We
therefore write
. We
therefore write
 to mean that formula
to mean that formula  holds at the
holds at the  -th stage of an arbitrary sequence
-th stage of an arbitrary sequence
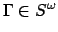 , relative to behaviour
, relative to behaviour  . Defining
. Defining
 is the
first step in our description of the semantics:
is the
first step in our description of the semantics:
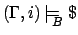 iff
iff

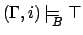
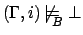
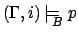 , for
, for  , iff
, iff 
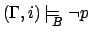 , for
, for  , iff
, iff

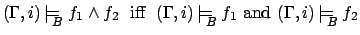
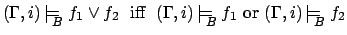
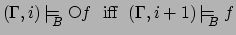
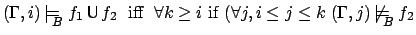 )
)
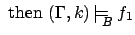 Note that except for subscript
Note that except for subscript  and for the first rule, this is
just the standard FLTL semantics, and that therefore $-free
formulae keep their FLTL meaning. As with FLTL, we say
and for the first rule, this is
just the standard FLTL semantics, and that therefore $-free
formulae keep their FLTL meaning. As with FLTL, we say
 iff
iff
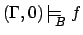 , and
, and
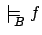 iff
iff
 for all
for all
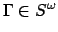 .
The modelling relation
.
The modelling relation
 can be seen as specifying when a
formula holds, on which reading it takes
can be seen as specifying when a
formula holds, on which reading it takes  as input. Our next and
final step is to use the
as input. Our next and
final step is to use the
 relation to define, for a
formula
relation to define, for a
formula  , the behaviour
, the behaviour  that it represents, and for this we
must rather assume that
that it represents, and for this we
must rather assume that  holds, and then solve for
holds, and then solve for  .
For instance, let
.
For instance, let  be
be
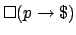 , i.e., we get
rewarded every time
, i.e., we get
rewarded every time  is true. We would like
is true. We would like  to be the set of
all finite sequences ending with a state containing
to be the set of
all finite sequences ending with a state containing  . For an
arbitrary
. For an
arbitrary  , we take
, we take  to be the set of prefixes that
have to be rewarded if
to be the set of prefixes that
have to be rewarded if  is to hold in all sequences:
is to hold in all sequences:
To understand Definition 2, recall that  contains
prefixes at the end of which we get a reward and $ evaluates to
true. Since
contains
prefixes at the end of which we get a reward and $ evaluates to
true. Since  is supposed to describe the way rewards will be
received in an arbitrary sequence, we are interested in
behaviours
is supposed to describe the way rewards will be
received in an arbitrary sequence, we are interested in
behaviours  which make $ true in such a way as to make
which make $ true in such a way as to make  hold without imposing constraints on the evolution of the world.
However, there may be many behaviours with this property, so we take
their intersection,3ensuring that
hold without imposing constraints on the evolution of the world.
However, there may be many behaviours with this property, so we take
their intersection,3ensuring that  will only reward a prefix if it has to because
that prefix is in every behaviour satisfying
will only reward a prefix if it has to because
that prefix is in every behaviour satisfying  . In all but
pathological cases (see Section 3.4), this makes
. In all but
pathological cases (see Section 3.4), this makes  coincide with the (set-inclusion) minimal behaviour
coincide with the (set-inclusion) minimal behaviour  such that
such that
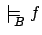 . The reason for this `stingy' semantics, making
rewards minimal, is that
. The reason for this `stingy' semantics, making
rewards minimal, is that  does not actually say that rewards are
allocated to more prefixes than are required for its truth. For
instance,
does not actually say that rewards are
allocated to more prefixes than are required for its truth. For
instance,
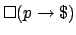 says only that a reward
is given every time
says only that a reward
is given every time  is true, even though a more generous
distribution of rewards would be consistent with it.
Sylvie Thiebaux
2006-01-20
is true, even though a more generous
distribution of rewards would be consistent with it.
Sylvie Thiebaux
2006-01-20
![]() iff
iff
![]()
![]()
![]()
![]() , for
, for ![]() , iff
, iff ![]()
![]() , for
, for ![]() , iff
, iff
![]()
![]()
![]()
![]()
![]() )
)
![]() Note that except for subscript
Note that except for subscript ![]() and for the first rule, this is
just the standard FLTL semantics, and that therefore $-free
formulae keep their FLTL meaning. As with FLTL, we say
and for the first rule, this is
just the standard FLTL semantics, and that therefore $-free
formulae keep their FLTL meaning. As with FLTL, we say
![]() iff
iff
![]() , and
, and
![]() iff
iff
![]() for all
for all
![]() .
The modelling relation
.
The modelling relation
![]() can be seen as specifying when a
formula holds, on which reading it takes
can be seen as specifying when a
formula holds, on which reading it takes ![]() as input. Our next and
final step is to use the
as input. Our next and
final step is to use the
![]() relation to define, for a
formula
relation to define, for a
formula ![]() , the behaviour
, the behaviour ![]() that it represents, and for this we
must rather assume that
that it represents, and for this we
must rather assume that ![]() holds, and then solve for
holds, and then solve for ![]() .
For instance, let
.
For instance, let ![]() be
be
![]() , i.e., we get
rewarded every time
, i.e., we get
rewarded every time ![]() is true. We would like
is true. We would like ![]() to be the set of
all finite sequences ending with a state containing
to be the set of
all finite sequences ending with a state containing ![]() . For an
arbitrary
. For an
arbitrary ![]() , we take
, we take ![]() to be the set of prefixes that
have to be rewarded if
to be the set of prefixes that
have to be rewarded if ![]() is to hold in all sequences:
is to hold in all sequences: