Reward Normality
$FLTL is therefore quite expressive. Unfortunately, it is rather
too expressive, in that it contains formulae which describe
``unnatural'' allocations of rewards. For instance, they may make
rewards depend on future behaviours rather than on the past, or they
may leave open a choice as to which of several behaviours is to
be rewarded.5An example of dependence on the future is
 , which
stipulates a reward now if
, which
stipulates a reward now if  is going to hold next.
We call such formula reward-unstable. What a reward-stable
is going to hold next.
We call such formula reward-unstable. What a reward-stable  amounts to is that whether a particular prefix needs to be rewarded in
order to make
amounts to is that whether a particular prefix needs to be rewarded in
order to make  true does not depend on the future of the sequence.
An example of an open choice of which behavior to reward
is
true does not depend on the future of the sequence.
An example of an open choice of which behavior to reward
is
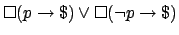 which says we should
either reward all achievements of the goal
which says we should
either reward all achievements of the goal  or reward
achievements of
or reward
achievements of 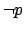 but does not determine which. We call such
formula reward-indeterminate. What a reward-determinate
but does not determine which. We call such
formula reward-indeterminate. What a reward-determinate  amounts to is that the set of behaviours modelling
amounts to is that the set of behaviours modelling  , i.e.
, i.e.
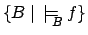 , has a unique minimum. If it does not,
, has a unique minimum. If it does not,  is
insufficient (too small) to make
is
insufficient (too small) to make  true.
In investigating $FLTL [41],
we examine the notions of reward-stability and
reward-determinacy in depth, and motivate the claim that formulae that
are both reward-stable and reward-determinate - we call them
reward-normal - are precisely those that capture the notion of
``no funny business''. This is the intuition that we ask the reader
to note, as it will be needed in the rest of the paper. Just for
reference then, we define:
true.
In investigating $FLTL [41],
we examine the notions of reward-stability and
reward-determinacy in depth, and motivate the claim that formulae that
are both reward-stable and reward-determinate - we call them
reward-normal - are precisely those that capture the notion of
``no funny business''. This is the intuition that we ask the reader
to note, as it will be needed in the rest of the paper. Just for
reference then, we define:
Definition 3
 is reward-normal iff for every
is reward-normal iff for every
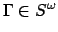 and every
and every
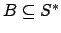 ,
,
 iff for every
iff for every
 , if
, if
 then
then
 .
.
The property of reward-normality is decidable
[41]. In Appendix A we give some
simple syntactic constructions guaranteed to result in reward-normal
formulae.
While reward-abnormal formulae may be interesting, for present
purposes we restrict attention to reward-normal ones. Indeed, we
stipulate as part of our method that only reward-normal formulae
should be used to represent behaviours.
Naturally, all formulae in Section 3.3 are normal.
Sylvie Thiebaux
2006-01-20