Conclusion, Related, and Future Work
In this paper, we have examined the problem of solving decision
processes with non-Markovian rewards. We have described existing
approaches which exploit a compact representation of the reward
function to automatically translate the NMRDP into an equivalent
process amenable to MDP solution methods. The computational model
underlying this framework can be traced back to work on the
relationship between linear temporal logic and automata in the areas
of automated verification and model-checking
[48,49]. While remaining in this framework, we
have proposed a new representation of non-Markovian reward functions
and a translation into MDPs aimed at making the best possible use of
state-based anytime heuristic search as the solution method. Our
representation extends future linear temporal logic to express
rewards. Our translation has the effect of embedding model-checking in
the solution method. It results in an MDP of the minimal size
achievable without stepping outside the anytime framework, and
consequently in better policies by the deadline. We have described
NMRDPP, a software platform that implements such approaches under a
common interface, and which proved a useful tool in their experimental
analysis. Both the system and the analysis are the first of their
kind. We were able to identify a number of general trends in the
behaviours of the methods and to provide advice as to which are the
best suited to certain circumstances. For obvious reasons, our
analysis has focused on artificial domains. Additional work should
examine a wider range of domains of more practical interest, to
see what form these results take in that context. Ultimately,
we would like our analysis to help NMRDPP automatically select
the most appropriate method. Unfortunately,
because of the difficulty of translating between PLTL and $FLTL,
it is likely that NMRDPP would still have to maintain both a
PLTL and a $FLTL version of the reward formulae.
A detailed comparison of our approach to solving NMRDPs with existing
methods [2,3]
can be found in Sections 3.10 and 5. Two important aspects of future work would
help take the comparison further. One is to settle the question of
the appropriateness of our translation to structured solution methods.
Symbolic implementations of the solution methods we consider, e.g.
symbolic LAO* [21], as well as formula progression in
the context of symbolic state representations
[40] could be investigated for that
purpose. The other is to take advantage of the greater expressive
power of $FLTL to consider a richer class of decision processes, for
instance with uncertainty as to which rewards are received and when.
Many extensions of the language are possible: adding eventualities,
unrestricted negation, first-class reward propositions, quantitative
time, etc. Of course, dealing with them via progression without
backtracking is another matter.
We should investigate the precise relationship between our line of
work and recent work on planning for temporally extended goals in
non-deterministic domains. Of particular interest are `weak'
temporally extended goals such as those expressible in the Eagle
language [16], and temporally extended goals
expressible in  -CTL* [7]. Eagle enables the
expression of attempted reachability and maintenance goals of the form
``try-reach
-CTL* [7]. Eagle enables the
expression of attempted reachability and maintenance goals of the form
``try-reach  '' and ``try-maintain
'' and ``try-maintain  '', which add to the goals
``do-reach
'', which add to the goals
``do-reach  '' and ``do-maintain
'' and ``do-maintain  '' already expressible in
CTL. The idea is that the generated policy should make every attempt
at satisfying proposition
'' already expressible in
CTL. The idea is that the generated policy should make every attempt
at satisfying proposition  . Furthermore, Eagle includes recovery
goals of the form ``
. Furthermore, Eagle includes recovery
goals of the form ``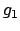 fail
fail 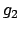 '', meaning that goal
'', meaning that goal 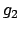 must
be achieved whenever goal
must
be achieved whenever goal 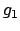 fails, and cyclic goals of the form
``repeat
fails, and cyclic goals of the form
``repeat  '', meaning that
'', meaning that  should be achieved cyclically until
it fails. The semantics of these goals is given in terms of variants
of Büchi tree automata with preferred transitions. Dal Lago et al. [16] present a planning algorithm based on
symbolic model-checking which generates policies achieving those
goals. Baral and Zhao [7] describe
should be achieved cyclically until
it fails. The semantics of these goals is given in terms of variants
of Büchi tree automata with preferred transitions. Dal Lago et al. [16] present a planning algorithm based on
symbolic model-checking which generates policies achieving those
goals. Baral and Zhao [7] describe  -CTL*,
an alternative framework for expressing a subset of Eagle goals and a
variety of others.
-CTL*,
an alternative framework for expressing a subset of Eagle goals and a
variety of others.  -CTL* is a variant of CTL* which allows for
formulae involving two types of path quantifiers: quantifiers tied to
the paths feasible under the generated policy, as is usual, but also
quantifiers more generally tied to the paths feasible under any of the
domain actions. Baral and Zhao [7] do not
present any planning algorithm. It would be very interesting to know
whether Eagle and
-CTL* is a variant of CTL* which allows for
formulae involving two types of path quantifiers: quantifiers tied to
the paths feasible under the generated policy, as is usual, but also
quantifiers more generally tied to the paths feasible under any of the
domain actions. Baral and Zhao [7] do not
present any planning algorithm. It would be very interesting to know
whether Eagle and  -CTL* goals can be encoded as non-Markovian
rewards in our framework. An immediate consequence would be that
NMRDPP could be used to plan for them. More generally, we would
like to examine the respective merits of non-deterministic planning
for temporally extended goals and decision-theoretic planning with
non-Markovian rewards.
In the pure probabilistic setting (no rewards), recent related
research includes work on planning and controller synthesis for
probabilistic temporally extended goals expressible in probabilistic
temporal logics such as CSL or PCTL
[52,6]. These logics enable
expressing statements about the probability of the policy satisfying a
given temporal goal exceeding a given threshold. For instance, Younes
and Simmons [52] describe a very general
probabilistic planning framework, involving concurrency, continuous
time, and temporally extended goals, rich enough to model generalised
semi-Markov processes. The solution algorithms are not directly
comparable to those presented here.
Another exciting future work area is the investigation of temporal
logic formalisms for specifying heuristic functions for NMRDPs or more
generally for search problems with temporally extended goals. Good
heuristics are important to some of the solution methods we are
targeting, and surely their value ought to depend on history. The
methods we have described could be applicable to the description and
processing of such heuristics. Related to this is the problem of
extending search control knowledge to fully operate under the
presence of temporally extended goals, rewards, and stochastic
actions. A first issue is that branching or probabilistic logics such
as CTL or PCTL variants should be preferred to FLTL when describing
search control knowledge, because when stochastic actions are
involved, search control often needs to refer to some of the
possible futures and even to their probabilities.18 Another major problem is
that the GOALP modality, which is the key to the specification of
reusable search control knowledge is interpreted with respect to a
fixed reachability goal19[5], and as such, is not applicable to domains
with temporally extended goals, let alone
rewards. Kabanza and Thiébaux [33]
present a first approach to
search control in the presence of temporally extended goals in
deterministic domains, but much remains to be done for a system like
NMRDPP to be able to support a meaningful extension of GOALP.
Finally, let us mention that related work in the area of databases
uses a similar approach to PLTLSTR to extend a database with
auxiliary relations containing sufficient information to check
temporal integrity constraints [15]. The issues are
somewhat different from those raised by NMRDPs: as there is only ever
one sequence of databases, what matters is more the size of these
auxiliary relations than avoiding making redundant distinctions.
Sylvie Thiebaux
2006-01-20
-CTL* goals can be encoded as non-Markovian
rewards in our framework. An immediate consequence would be that
NMRDPP could be used to plan for them. More generally, we would
like to examine the respective merits of non-deterministic planning
for temporally extended goals and decision-theoretic planning with
non-Markovian rewards.
In the pure probabilistic setting (no rewards), recent related
research includes work on planning and controller synthesis for
probabilistic temporally extended goals expressible in probabilistic
temporal logics such as CSL or PCTL
[52,6]. These logics enable
expressing statements about the probability of the policy satisfying a
given temporal goal exceeding a given threshold. For instance, Younes
and Simmons [52] describe a very general
probabilistic planning framework, involving concurrency, continuous
time, and temporally extended goals, rich enough to model generalised
semi-Markov processes. The solution algorithms are not directly
comparable to those presented here.
Another exciting future work area is the investigation of temporal
logic formalisms for specifying heuristic functions for NMRDPs or more
generally for search problems with temporally extended goals. Good
heuristics are important to some of the solution methods we are
targeting, and surely their value ought to depend on history. The
methods we have described could be applicable to the description and
processing of such heuristics. Related to this is the problem of
extending search control knowledge to fully operate under the
presence of temporally extended goals, rewards, and stochastic
actions. A first issue is that branching or probabilistic logics such
as CTL or PCTL variants should be preferred to FLTL when describing
search control knowledge, because when stochastic actions are
involved, search control often needs to refer to some of the
possible futures and even to their probabilities.18 Another major problem is
that the GOALP modality, which is the key to the specification of
reusable search control knowledge is interpreted with respect to a
fixed reachability goal19[5], and as such, is not applicable to domains
with temporally extended goals, let alone
rewards. Kabanza and Thiébaux [33]
present a first approach to
search control in the presence of temporally extended goals in
deterministic domains, but much remains to be done for a system like
NMRDPP to be able to support a meaningful extension of GOALP.
Finally, let us mention that related work in the area of databases
uses a similar approach to PLTLSTR to extend a database with
auxiliary relations containing sufficient information to check
temporal integrity constraints [15]. The issues are
somewhat different from those raised by NMRDPs: as there is only ever
one sequence of databases, what matters is more the size of these
auxiliary relations than avoiding making redundant distinctions.
Sylvie Thiebaux
2006-01-20