Random Problem Domains
Random problem domains are produced by first creating a random action
specification defining the domain dynamics. Some of the experiments
we conducted20 also involved producing, in a second step, a random reward
specification that had desired properties in relation to the generated
dynamics.
The random generation of the domain dynamics takes as parameters the
number  of propositions in the domain and the number of actions to be
produced, and starts by assigning some effects to each action such
that each proposition is affected by exactly one action. For example,
if we have 5 actions and 14 propositions, the first 4 actions may
affect 3 propositions each, the 5th one only 2, and the affected
propositions are all different. Once each action has
some initial effects, we continue to add more effects one at a time,
until a sufficient proportion of the state space is reachable - see
``proportion reachable'' parameter below.
Each additional effect is generated by picking up a random action
and a random proposition, and producing a random decision
diagram according to the ``uncertainty'' and ``structure'' parameters
below:
of propositions in the domain and the number of actions to be
produced, and starts by assigning some effects to each action such
that each proposition is affected by exactly one action. For example,
if we have 5 actions and 14 propositions, the first 4 actions may
affect 3 propositions each, the 5th one only 2, and the affected
propositions are all different. Once each action has
some initial effects, we continue to add more effects one at a time,
until a sufficient proportion of the state space is reachable - see
``proportion reachable'' parameter below.
Each additional effect is generated by picking up a random action
and a random proposition, and producing a random decision
diagram according to the ``uncertainty'' and ``structure'' parameters
below:
- The Uncertainty
parameter is the probability of a non zero/one
value as a leaf node. An uncertainty of 1 will result in all leaf
nodes having random values from a uniform distribution. An uncertainty
of 0 will result in all leaf nodes having values 0 or 1 with an equal
probability.
- The Structure (or influence)
parameter is the probability of a decision diagram
containing a particular proposition. So an influence of 1 will
result in all decision diagrams including all
propositions (and very unlikely to have significant structure),
while 0 will result in decision diagrams that
do not depend on the values of propositions.
- The Proportion Reachable parameter is a lower bound on the
proportion of the entire
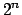 state space that is reachable from
the start state. The algorithm adds behaviour until this lower bound
is reached. A value of 1 will result in the algorithm running until
the actions are sufficient to allow the entire state space to be
reachable.
state space that is reachable from
the start state. The algorithm adds behaviour until this lower bound
is reached. A value of 1 will result in the algorithm running until
the actions are sufficient to allow the entire state space to be
reachable.
A reward specification can be produced with regard to the generated
dynamics such that a specified number of the rewards are reachable and
a specified number are unreachable. First, a decision diagram is
produced to represent which states are reachable and which are not,
given the domain dynamics. Next, a random path is taken from the root
of this decision diagram to a true terminal if we are generating an
attainable reward, or a false terminal if we are producing an
unattainable reward. The propositions encountered on this path, both
negated and not, form a conjunction that is the reward formula. This process
is repeated until the desired number of reachable and unreachable
rewards are obtained.
Sylvie Thiebaux
2006-01-20