The Algorithm

Figure 9 shows the final algorithm. At the beginning it proceeds just like the basic or integrative windowing algorithms described earlier in this paper. It selects a random subset of the examples, learns a theory from these examples, and tests it on the remaining examples. Like integrative windowing, it does not merely add examples that have been incorrectly classified to the window for the next iteration, but it also removes all examples from this window that are covered by good rules. To determine good rules, it tests the individual rules that have been learned from the current window on the entire data set and performs the consistency check described in section 5.2.1 (procedure SIGNIFICANT). If the rule passes the test, it is added to the final theory, and all examples that are covered by it are removed from the training set (and the window). Otherwise, the examples covered by this rule become candidates for being added to the window in the next iteration. After all uncovered positive examples have also been added to this candidate set, the algorithm randomly selects MaxIncSize examples that are added to the window. Not shown in the algorithm is the completeness check described in section 5.2.2, which doubles the window size if the noise-tolerant learner does not find any rules.

  

Figure 9: A noise-tolerant version of integrative windowing.

With a setting of 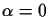$\alpha = 0$, NOISETOLERANTWINDOWING is very similar to the INTEGRATIVEWINDOWING algorithm of Figure 3, with the difference that the latter only tests a theory until it has collected MaxIncSize new examples to add to the current window. Thus it cannot determine whether a rule has already been tested on all examples and has to test the stored rules in all subsequent iterations. NOISETOLERANTWINDOWING, on the other hand, tests a rule on the entire training set. If it finds the rule to be significant it will add it to the final rule set and will never test it again. Consequently, the examples covered by such a rule can be removed not only from the window, but from the entire training set.