Parallel Operations on Sequences

NESL supports parallelism through operations on sequences, which are specified using square brackets. For example

 [2, 1, 9, -3]  

is a sequence of four integers. In NESL all elements of a sequence must be of the same type, and all sequences must be of finite length. Parallelism on sequences can be achieved in two ways: the ability to apply any function concurrently over each element of a sequence, and a set of built-in parallel functions that operate on sequences. The application of a function over a sequence is achieved using set-like notation similar to set-formers in SETL [40] and list-comprehensions in Miranda [43] and Haskell [28]. For example, the expression

negates each elements of the sequence [3, -4, -9, 5]. This construct can be read as ``in parallel for each a in the sequence , negate a''. The symbol points to the result of the expression, and the expression [int] specifies the type of the result: a sequence of integers. The semantics of the notation differs from that of SETL, Miranda or Haskell in that the operation is defined to be applied in parallel. Henceforth we will refer to the notation as the apply-to-each construct. As with set comprehensions, the apply-to-each construct also provides the ability to subselect elements of a sequence: the expression

can be read as, ``in parallel for each a in the sequence such that a is less than 4, negate a''. The elements that remain maintain their order relative to each other. It is also possible to iterate over multiple sequences. The expression

adds the two sequences elementwise. A full description of the apply-to-each construct is given in Section 3.2.

  
Table: List of some of the sequence functions supplied by NESL. In the work column, S(v) refers to the size of the object v. The * before certain functions means that those functions are primitives. All the other functions can be built out of the primitives with at most a constant factor overhead in both work and depth. For _scan the can be one of {plus, max, min, or, and}. All the sequence functions are described in detail in Appendix B.2. In rep and <-, the work complexity depends on whether the variable used for d is the final reference to that variable (arguments are evaluated left to right). If it is the final reference, then the complexity before the comma is used, otherwise the complexity after the comma is used.

In NESL, any function, whether primitive or user defined, can be applied to each element of a sequence. So, for example, we could define a factorial function

and then apply it over the elements of a sequence

In this example, the function name(arguments) = body; construct is used to define factorial. The function is of type int -> int, indicating a function that maps integers to integers. The type is inferred by the compiler.

An apply-to-each construct applies a body to each element of a sequence. We will call each such application an instance. Since there are no side effects in NESL, there is no way to communicate among the instances of an apply-to-each. An implementation can therefore execute the instances in any order it chooses without changing the result. In particular, the instances can be implemented in parallel, therefore giving the apply-to-each its parallel semantics.

In addition to the apply-to-each construct, a second way to take advantage of parallelism in NESL is through a set of sequence functions. The sequence functions operate on whole sequences and all have relatively simple parallel implementations. For example the function sum sums the elements of a sequence.

Since addition is associative, this can be implemented on a parallel machine in logarithmic time using a tree. Another common sequence function is the permute function, which permutes a sequence based on a second sequence of indices. For example:

In this case, the 4 characters of the string "nesl" (the term string is used to refer to a sequence of characters) are permuted to the indices [2, 1, 3, 0] (n 2, e 1, s 3, and l 0). The implementation of the permute function on a distributed-memory parallel machine could use its communication network and the implementation on a shared-memory machine could use an indirect write into the memory.

Table 1 lists some of the sequence functions available in NESL. A subset of the functions (the starred ones) form a complete set of primitives. These primitives, along with the scalar operations and the apply-to-each construct, are sufficient for implementing the other functions in the table with at most a constant factor increase in both the work and depth complexities, as defined in Section 1.5. The table also lists the work complexity of each function, which will also be defined in Section 1.5.

  
Figure: An implementation of order statistics. The function kth_smallest returns the kth smallest element from the input sequence s.

We now consider an example of the use of sequences in NESL. The algorithm we consider solves the problem of finding the k smallest element in a set s, using a parallel version of the quickorder algorithm [26].   Quickorder is similar to quicksort, but only calls itself recursively on either the elements lesser or greater than the pivot. The NESL\ code for the algorithm is shown in Figure 1. The let construct is used to bind local variables (see Section 3.2.2 for more details.). The code first binds len to the length of the input sequence s, and then extracts the middle element of s as a pivot. The algorithm then selects all the elements less than the pivot, and places them in a sequence that is bound to lesser. For example:

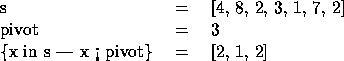
After the pack, if the number of elements in the set lesser is greater than k, then the k smallest element must belong to that set. In this case, the algorithm calls kth_smallest recursively on lesser using the same k. Otherwise, the algorithm selects the elements that are greater than the pivot, again using pack, and can similarly find if the k element belongs in the set greater. If it does belong in greater, the algorithm calls itself recursively, but must now readjust k by subtracting off the number of elements lesser and equal to the pivot. If the k element belongs in neither lesser nor greater, then it must be the pivot, and the algorithm returns this value.