



Next: Concluding remarks
Up: Performance of task assignment
Previous: Stability
Contents
Mean response time
Figure 5.3:
Mean response time of short jobs and long jobs under
Dedicated, SBCS-ID, and SBCS-ID.
Job sizes have exponential distributions.
How shorts gain from cycle stealing - 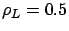
How longs suffer from cycle stealing - 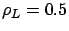
(a)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=1$](img1332.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 10$](img1227.png) |
(b)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=1$](img1332.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png) |
(c)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=10$](img1335.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png)
(pathological case)
|
|
Figure 5.3 illustrates the benefit to the short
jobs and the penalty to the long jobs under SBCS-ID and SBCS-CQ for three job size configurations: (a) ``short'' jobs are (10 times) shorter in expectation,
(b) ``short'' jobs and ``long'' jobs are indistinguishable,
and (c) ``short'' jobs are (10 times) longer in expectation.
Here, we assume that both the short jobs and the long jobs have exponential distributions.
The mean response time of the short jobs (respectively, long
jobs) is plotted as a function of  in the top row
(respectively, bottom row). In this figure, we fix
in the top row
(respectively, bottom row). In this figure, we fix 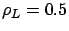 , and
consider the full range of
, and
consider the full range of  . Recall from
Section 5.4.2 that Dedicated leads to instability when
. Recall from
Section 5.4.2 that Dedicated leads to instability when
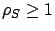 . However for SBCS-CQ,
. However for SBCS-CQ,  is allowed as
high as
is allowed as
high as 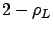 , and for SBCS-ID,
, and for SBCS-ID,  is allowed as high
as some intermediate value shown in Figure 5.2, which
is not as high as
is allowed as high
as some intermediate value shown in Figure 5.2, which
is not as high as 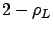 and yet is higher than Dedicated.
and yet is higher than Dedicated.
Figure 5.3(a) (top row) shows that
the short jobs benefit tremendously from cycle stealing. For 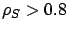 , the mean improvement of cycle stealing algorithms over Dedicated is over an order of magnitude. As
, the mean improvement of cycle stealing algorithms over Dedicated is over an order of magnitude. As
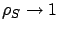 , the mean response time under Dedicated goes to
infinity, whereas it is 5.3 under SBCS-ID and 4.3 under SBCS-CQ.
This shows the huge benefit that short jobs obtain by being able to
steal idle cycles from the long host.
, the mean response time under Dedicated goes to
infinity, whereas it is 5.3 under SBCS-ID and 4.3 under SBCS-CQ.
This shows the huge benefit that short jobs obtain by being able to
steal idle cycles from the long host.
Figure 5.3(a) (top row) shows that the improvement
of SBCS-CQ over SBCS-ID is also vast. As
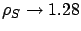 , the mean response time under SBCS-ID goes to infinity
whereas it is approximately 15.5 under SBCS-CQ. This follows as
under SBCS-ID only new short arrivals can benefit from idle
cycles, whereas under SBCS-CQ waiting short jobs may benefit.
, the mean response time under SBCS-ID goes to infinity
whereas it is approximately 15.5 under SBCS-CQ. This follows as
under SBCS-ID only new short arrivals can benefit from idle
cycles, whereas under SBCS-CQ waiting short jobs may benefit.
Figure 5.3(a) (bottom row) shows that the
penalty imposed on the long jobs by cycle stealing is relatively small.
The penalty increases with  , but even when
, but even when 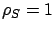 , the
penalty to the long jobs is only 2.5% under SBCS-CQ and 3.0% under
SBCS-ID. This is in contrast to the unbounded improvement for the
short jobs.
, the
penalty to the long jobs is only 2.5% under SBCS-CQ and 3.0% under
SBCS-ID. This is in contrast to the unbounded improvement for the
short jobs.
Figure 5.3(b) shows the case when the short
jobs and the long jobs are indistinguishable, and
Figure 5.3(c) shows the pathological case where
the ``short'' jobs have longer expected size than the ``long'' jobs.
We see that trends are similar to column (a), with only the absolute
magnitude of the numbers growing. Specifically, when the ``short''
jobs are longer or when the ``long'' jobs are shorter, both the
benefit to the ``short'' jobs and the penalty to the ``long'' jobs
become greater. Greater penalty to the ``long'' jobs is to be
expected since a ``long'' job may get stuck behind a ``short'' job
whose size is in fact ten time longer in expectation.
Greater benefit to the ``short'' jobs may be explained as a counter effect
to the greater penalty to the ``long'' jobs. Specifically,
when the ``long'' jobs are shorter, the busy period of the ``long'' server
is shorter, which allows the ``long'' server to help the ``short'' jobs more
frequently (although the duration of the help is also shorter);
at the beginning of the busy period, the ``long'' server may be serving
the ``short'' jobs, and this implies that ``short'' jobs may utilize
more nonidle cycles of the ``long'' server.
One interesting observation is that the penalty to the long jobs appears
lower under SBCS-CQ than under SBCS-ID. At first this seems
quite contrary, since under SBCS-CQ more cycles are given to
the short jobs; thus it is reasonable to expect the long jobs should
suffer more. The reason this is not true is that under SBCS-CQ
the servers are re-namable. Thus a long job arriving to find both
servers serving short jobs need only wait for the first of the
two servers to free up under SBCS-CQ.
Figure 5.4:
Percentage change in the overall mean response time of SBCS-ID and SBCS-CQ against Dedicated.
Job sizes have exponential distributions.
Percentage improvement over Dedicated - 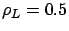
Percentage improvement over Dedicated - 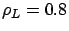
(a)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=1$](img1332.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 10$](img1227.png) |
(b)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=1$](img1332.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png) |
(c)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=10$](img1335.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png)
(pathological case)
|
|
Figure 5.4 illustrates the percentage improvement of
the SBCS-ID and SBCS-CQ over the Dedicated with respect
to the overall mean response time. The percentage change (in
overall mean response time) against the Dedicated is plotted as a
function of  for SBCS-ID and SBCS-CQ. In the top row
(respectively, bottom row),
for SBCS-ID and SBCS-CQ. In the top row
(respectively, bottom row), 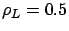 (respectively,
(respectively, 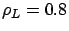 )
is fixed. Namely, in the top row, the parameter settings are exactly
the same as in Figure 5.3, while
)
is fixed. Namely, in the top row, the parameter settings are exactly
the same as in Figure 5.3, while  is
set higher in the bottom row. Again, three columns correspond to
three job size configurations.
is
set higher in the bottom row. Again, three columns correspond to
three job size configurations.
Figure 5.4(a) shows that SBCS-ID and SBCS-CQ improves upon Dedicated with respect to the overall
mean response time throughout the range of load,  , for both
low
, for both
low  (top row) and high
(top row) and high  (bottom row).
As
(bottom row).
As  becomes higher, the improvement over Dedicate becomes
greater.
At
becomes higher, the improvement over Dedicate becomes
greater.
At 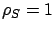 , Dedicated becomes unstable, and
the percentage change in the overall mean response time is
, Dedicated becomes unstable, and
the percentage change in the overall mean response time is 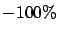 for both SBCS-ID
and SBCS-CQ, which still provide finite overall mean response time at
for both SBCS-ID
and SBCS-CQ, which still provide finite overall mean response time at 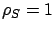 .
(In fact, although not clear from the figure, the overall mean
response time under SBCS-ID is slightly worse (within 0.1%) than
that under Dedicated at very low load (
.
(In fact, although not clear from the figure, the overall mean
response time under SBCS-ID is slightly worse (within 0.1%) than
that under Dedicated at very low load (
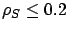 ). By
contrast, the overall mean response time under SBCS-CQ is always
lower than that under Dedicated with these parameter settings.)
). By
contrast, the overall mean response time under SBCS-CQ is always
lower than that under Dedicated with these parameter settings.)
Figure 5.4(b) shows that SBCS-CQ improves upon
Dedicated with respect to the overall mean response time for all
 , for both low
, for both low  (top row) and high
(top row) and high  (bottom
row), even if the short jobs and long jobs are indistinguishable.
Again, the improvement over Dedicate becomes greater as
(bottom
row), even if the short jobs and long jobs are indistinguishable.
Again, the improvement over Dedicate becomes greater as  becomes higher. On the other hand, the overall mean response time
under SBCS-ID is slightly worse (within 5%) than that under Dedicated at low load (specifically,
becomes higher. On the other hand, the overall mean response time
under SBCS-ID is slightly worse (within 5%) than that under Dedicated at low load (specifically, 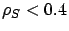 for
for 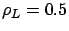 (top row) and
(top row) and 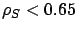 for
for 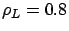 (bottom row)). This
makes intuitive sense, since SBCS-ID sends more jobs to the server with
higher load if
(bottom row)). This
makes intuitive sense, since SBCS-ID sends more jobs to the server with
higher load if 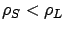 . Overall, as long as
. Overall, as long as
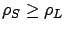 , both SBCS-ID and SBCS-CQ provides
significant improvement over Dedicated, and this improvement
becomes greater at higher
, both SBCS-ID and SBCS-CQ provides
significant improvement over Dedicated, and this improvement
becomes greater at higher  and becomes unbounded at
and becomes unbounded at
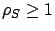 .
.
Figure 5.4(c) shows that when the ``short'' jobs are
longer than the ``long'' jobs (in the pathological case), the overall
mean response time under both SBCS-ID and SBCS-CQ can be
higher than that under Dedicated, but for high enough  ,
SBCS-ID and SBCS-CQ can still provide unbounded benefit over
Dedicated. In the figure, SBCS-CQ improves upon Dedicated if
,
SBCS-ID and SBCS-CQ can still provide unbounded benefit over
Dedicated. In the figure, SBCS-CQ improves upon Dedicated if 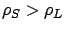 for both low
for both low  (top row) and high
(top row) and high
 (bottom row). (The advantage of SBCS-CQ does
not necessarily occur exactly at
(bottom row). (The advantage of SBCS-CQ does
not necessarily occur exactly at 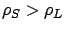 . For
example, when
. For
example, when
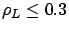 , SBCS-CQ improves upon Dedicated for all
, SBCS-CQ improves upon Dedicated for all  ). On the other hand, SBCS-ID improves
upon Dedicated only at high
). On the other hand, SBCS-ID improves
upon Dedicated only at high  , but again the improvement
of both SBCS-ID and SBCS-CQ becomes greater at higher
, but again the improvement
of both SBCS-ID and SBCS-CQ becomes greater at higher
 and becomes unbounded at
and becomes unbounded at 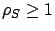 .
.
Figure 5.4 shows that at higher  (bottom
row), both the benefit to the short jobs and the penalty to the long jobs are
reduced, and overall the improvement (or disimprovement) of SBCS-ID
and SBCS-CQ over Dedicated becomes smaller. This is to be
expected, as there are fewer idle cycles to steal at higher
(bottom
row), both the benefit to the short jobs and the penalty to the long jobs are
reduced, and overall the improvement (or disimprovement) of SBCS-ID
and SBCS-CQ over Dedicated becomes smaller. This is to be
expected, as there are fewer idle cycles to steal at higher  .
.
Figure 5.5:
Effect of variability in long job size on the mean response time.
|
Effect of increasing long job size variability on short performance
Effect of increasing long job size variability on long performance
Effect of increasing long job size variability on overall performance
(a)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=1$](img1332.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 10$](img1227.png) |
(b)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=1$](img1332.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png) |
(c)
![$\mbox{{\bf\sf E}}\left[ X_S \right]=10$](img1335.png) and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png)
(pathological case)
|
|
Figure 5.5 considers the effect of increasing the service
demand variability of the long jobs. The parameter settings are the same as
in Figure 5.3 and the top row of Figure 5.4,
except that two curves are shown for each of Dedicated, SBCS-ID, and SBCS-CQ,
corresponding to the case where the long jobs have a (two phase) PH distribution with 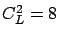 and the case where the long jobs have an exponential distribution5.1.
and the case where the long jobs have an exponential distribution5.1.
Theorem 9 implies that when 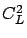 is increased
from 1 to 8, the mean response time of the long jobs under SBCS-ID and
under Dedicated increases by the same amount, and this can also
be verified in the middle row of Figure 5.5.
The figure also suggests that the the mean response time of the long jobs
under SBCS-CQ increases by approximately the same amount as Dedicated. Closer examination shows that the difference in the
increase in the mean response time of the long jobs between SBCS-CQ
and Dedicated is only at most 0.4% in (a), at most 0.03% in
(b), and at most 2.8% in (c), and the difference appears to be larger
when the error in the analysis of SBCS-CQ against simulation is
larger. Since the mean response time of the long jobs is higher with
higher
is increased
from 1 to 8, the mean response time of the long jobs under SBCS-ID and
under Dedicated increases by the same amount, and this can also
be verified in the middle row of Figure 5.5.
The figure also suggests that the the mean response time of the long jobs
under SBCS-CQ increases by approximately the same amount as Dedicated. Closer examination shows that the difference in the
increase in the mean response time of the long jobs between SBCS-CQ
and Dedicated is only at most 0.4% in (a), at most 0.03% in
(b), and at most 2.8% in (c), and the difference appears to be larger
when the error in the analysis of SBCS-CQ against simulation is
larger. Since the mean response time of the long jobs is higher with
higher 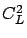 , the percentage penalty of the long jobs is therefore
considerably lessened when
, the percentage penalty of the long jobs is therefore
considerably lessened when 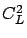 is increased.
is increased.
The top row of Figure 5.5 shows that increasing
long job size variability has surprisingly little impact on the mean
response time of the short jobs under SBCS-ID when  ,
although there is a noticeable impact when
,
although there is a noticeable impact when 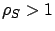 and the
``short'' jobs are shorter than the ``long'' jobs (column (a)). We
would have expected the opposite: that shorts would prefer less
variable long job sizes because that means less variable long busy
periods and more regular help. In fact, this expectation better
applies to SBCS-CQ: the mean response time of the short jobs under
SBCS-CQ increases more significantly by increasing long job size
variability. This makes intuitive sense, since the short jobs rely
on the help from the long server more under SBCS-CQ than
under SBCS-ID.
and the
``short'' jobs are shorter than the ``long'' jobs (column (a)). We
would have expected the opposite: that shorts would prefer less
variable long job sizes because that means less variable long busy
periods and more regular help. In fact, this expectation better
applies to SBCS-CQ: the mean response time of the short jobs under
SBCS-CQ increases more significantly by increasing long job size
variability. This makes intuitive sense, since the short jobs rely
on the help from the long server more under SBCS-CQ than
under SBCS-ID.
To summarize, we have seen that short jobs are tremendously helped by
cycle stealing, and that SBCS-CQ offers greater improvements to
short jobs than SBCS-ID. We have also seen that, provided that
``short'' jobs are no longer than ``long'' jobs, the penalty of cycle
stealing on long jobs is negligible. This penalty is greater under
SBCS-ID than under SBCS-CQ. Thus, SBCS-CQ is always
superior to SBCS-ID, and both are typically far better than Dedicated.




Next: Concluding remarks
Up: Performance of task assignment
Previous: Stability
Contents
Takayuki Osogami
2005-07-19
![]() in the top row
(respectively, bottom row). In this figure, we fix
in the top row
(respectively, bottom row). In this figure, we fix ![]() , and
consider the full range of
, and
consider the full range of ![]() . Recall from
Section 5.4.2 that Dedicated leads to instability when
. Recall from
Section 5.4.2 that Dedicated leads to instability when
![]() . However for SBCS-CQ,
. However for SBCS-CQ, ![]() is allowed as
high as
is allowed as
high as ![]() , and for SBCS-ID,
, and for SBCS-ID, ![]() is allowed as high
as some intermediate value shown in Figure 5.2, which
is not as high as
is allowed as high
as some intermediate value shown in Figure 5.2, which
is not as high as ![]() and yet is higher than Dedicated.
and yet is higher than Dedicated.
![]() , the mean improvement of cycle stealing algorithms over Dedicated is over an order of magnitude. As
, the mean improvement of cycle stealing algorithms over Dedicated is over an order of magnitude. As
![]() , the mean response time under Dedicated goes to
infinity, whereas it is 5.3 under SBCS-ID and 4.3 under SBCS-CQ.
This shows the huge benefit that short jobs obtain by being able to
steal idle cycles from the long host.
, the mean response time under Dedicated goes to
infinity, whereas it is 5.3 under SBCS-ID and 4.3 under SBCS-CQ.
This shows the huge benefit that short jobs obtain by being able to
steal idle cycles from the long host.
![]() , the mean response time under SBCS-ID goes to infinity
whereas it is approximately 15.5 under SBCS-CQ. This follows as
under SBCS-ID only new short arrivals can benefit from idle
cycles, whereas under SBCS-CQ waiting short jobs may benefit.
, the mean response time under SBCS-ID goes to infinity
whereas it is approximately 15.5 under SBCS-CQ. This follows as
under SBCS-ID only new short arrivals can benefit from idle
cycles, whereas under SBCS-CQ waiting short jobs may benefit.
![]() , but even when
, but even when ![]() , the
penalty to the long jobs is only 2.5% under SBCS-CQ and 3.0% under
SBCS-ID. This is in contrast to the unbounded improvement for the
short jobs.
, the
penalty to the long jobs is only 2.5% under SBCS-CQ and 3.0% under
SBCS-ID. This is in contrast to the unbounded improvement for the
short jobs.
![]() for SBCS-ID and SBCS-CQ. In the top row
(respectively, bottom row),
for SBCS-ID and SBCS-CQ. In the top row
(respectively, bottom row), ![]() (respectively,
(respectively, ![]() )
is fixed. Namely, in the top row, the parameter settings are exactly
the same as in Figure 5.3, while
)
is fixed. Namely, in the top row, the parameter settings are exactly
the same as in Figure 5.3, while ![]() is
set higher in the bottom row. Again, three columns correspond to
three job size configurations.
is
set higher in the bottom row. Again, three columns correspond to
three job size configurations.
![]() , for both
low
, for both
low ![]() (top row) and high
(top row) and high ![]() (bottom row).
As
(bottom row).
As ![]() becomes higher, the improvement over Dedicate becomes
greater.
At
becomes higher, the improvement over Dedicate becomes
greater.
At ![]() , Dedicated becomes unstable, and
the percentage change in the overall mean response time is
, Dedicated becomes unstable, and
the percentage change in the overall mean response time is ![]() for both SBCS-ID
and SBCS-CQ, which still provide finite overall mean response time at
for both SBCS-ID
and SBCS-CQ, which still provide finite overall mean response time at ![]() .
(In fact, although not clear from the figure, the overall mean
response time under SBCS-ID is slightly worse (within 0.1%) than
that under Dedicated at very low load (
.
(In fact, although not clear from the figure, the overall mean
response time under SBCS-ID is slightly worse (within 0.1%) than
that under Dedicated at very low load (
![]() ). By
contrast, the overall mean response time under SBCS-CQ is always
lower than that under Dedicated with these parameter settings.)
). By
contrast, the overall mean response time under SBCS-CQ is always
lower than that under Dedicated with these parameter settings.)
![]() , for both low
, for both low ![]() (top row) and high
(top row) and high ![]() (bottom
row), even if the short jobs and long jobs are indistinguishable.
Again, the improvement over Dedicate becomes greater as
(bottom
row), even if the short jobs and long jobs are indistinguishable.
Again, the improvement over Dedicate becomes greater as ![]() becomes higher. On the other hand, the overall mean response time
under SBCS-ID is slightly worse (within 5%) than that under Dedicated at low load (specifically,
becomes higher. On the other hand, the overall mean response time
under SBCS-ID is slightly worse (within 5%) than that under Dedicated at low load (specifically, ![]() for
for ![]() (top row) and
(top row) and ![]() for
for ![]() (bottom row)). This
makes intuitive sense, since SBCS-ID sends more jobs to the server with
higher load if
(bottom row)). This
makes intuitive sense, since SBCS-ID sends more jobs to the server with
higher load if ![]() . Overall, as long as
. Overall, as long as
![]() , both SBCS-ID and SBCS-CQ provides
significant improvement over Dedicated, and this improvement
becomes greater at higher
, both SBCS-ID and SBCS-CQ provides
significant improvement over Dedicated, and this improvement
becomes greater at higher ![]() and becomes unbounded at
and becomes unbounded at
![]() .
.
![]() ,
SBCS-ID and SBCS-CQ can still provide unbounded benefit over
Dedicated. In the figure, SBCS-CQ improves upon Dedicated if
,
SBCS-ID and SBCS-CQ can still provide unbounded benefit over
Dedicated. In the figure, SBCS-CQ improves upon Dedicated if ![]() for both low
for both low ![]() (top row) and high
(top row) and high
![]() (bottom row). (The advantage of SBCS-CQ does
not necessarily occur exactly at
(bottom row). (The advantage of SBCS-CQ does
not necessarily occur exactly at ![]() . For
example, when
. For
example, when
![]() , SBCS-CQ improves upon Dedicated for all
, SBCS-CQ improves upon Dedicated for all ![]() ). On the other hand, SBCS-ID improves
upon Dedicated only at high
). On the other hand, SBCS-ID improves
upon Dedicated only at high ![]() , but again the improvement
of both SBCS-ID and SBCS-CQ becomes greater at higher
, but again the improvement
of both SBCS-ID and SBCS-CQ becomes greater at higher
![]() and becomes unbounded at
and becomes unbounded at ![]() .
.
![]() (bottom
row), both the benefit to the short jobs and the penalty to the long jobs are
reduced, and overall the improvement (or disimprovement) of SBCS-ID
and SBCS-CQ over Dedicated becomes smaller. This is to be
expected, as there are fewer idle cycles to steal at higher
(bottom
row), both the benefit to the short jobs and the penalty to the long jobs are
reduced, and overall the improvement (or disimprovement) of SBCS-ID
and SBCS-CQ over Dedicated becomes smaller. This is to be
expected, as there are fewer idle cycles to steal at higher ![]() .
.
![]() and the case where the long jobs have an exponential distribution5.1.
and the case where the long jobs have an exponential distribution5.1.
![]() is increased
from 1 to 8, the mean response time of the long jobs under SBCS-ID and
under Dedicated increases by the same amount, and this can also
be verified in the middle row of Figure 5.5.
The figure also suggests that the the mean response time of the long jobs
under SBCS-CQ increases by approximately the same amount as Dedicated. Closer examination shows that the difference in the
increase in the mean response time of the long jobs between SBCS-CQ
and Dedicated is only at most 0.4% in (a), at most 0.03% in
(b), and at most 2.8% in (c), and the difference appears to be larger
when the error in the analysis of SBCS-CQ against simulation is
larger. Since the mean response time of the long jobs is higher with
higher
is increased
from 1 to 8, the mean response time of the long jobs under SBCS-ID and
under Dedicated increases by the same amount, and this can also
be verified in the middle row of Figure 5.5.
The figure also suggests that the the mean response time of the long jobs
under SBCS-CQ increases by approximately the same amount as Dedicated. Closer examination shows that the difference in the
increase in the mean response time of the long jobs between SBCS-CQ
and Dedicated is only at most 0.4% in (a), at most 0.03% in
(b), and at most 2.8% in (c), and the difference appears to be larger
when the error in the analysis of SBCS-CQ against simulation is
larger. Since the mean response time of the long jobs is higher with
higher ![]() , the percentage penalty of the long jobs is therefore
considerably lessened when
, the percentage penalty of the long jobs is therefore
considerably lessened when ![]() is increased.
is increased.
![]() ,
although there is a noticeable impact when
,
although there is a noticeable impact when ![]() and the
``short'' jobs are shorter than the ``long'' jobs (column (a)). We
would have expected the opposite: that shorts would prefer less
variable long job sizes because that means less variable long busy
periods and more regular help. In fact, this expectation better
applies to SBCS-CQ: the mean response time of the short jobs under
SBCS-CQ increases more significantly by increasing long job size
variability. This makes intuitive sense, since the short jobs rely
on the help from the long server more under SBCS-CQ than
under SBCS-ID.
and the
``short'' jobs are shorter than the ``long'' jobs (column (a)). We
would have expected the opposite: that shorts would prefer less
variable long job sizes because that means less variable long busy
periods and more regular help. In fact, this expectation better
applies to SBCS-CQ: the mean response time of the short jobs under
SBCS-CQ increases more significantly by increasing long job size
variability. This makes intuitive sense, since the short jobs rely
on the help from the long server more under SBCS-CQ than
under SBCS-ID.