



Next: Effect of thresholds
Up: Mean response time
Previous: Benefit of cycle stealing:
Contents
Effect of donor job size variability
For
 ,
variability of donor job sizes has very little effect on beneficiary mean response time.
,
variability of donor job sizes has very little effect on beneficiary mean response time.
For
 , we find variability of donor job sizes has very
little effect on beneficiary mean response time. This finding
surprised us; we expected the beneficiary to gain far less from the
bursty help of a donor with irregular (highly variable) job sizes.
, we find variability of donor job sizes has very
little effect on beneficiary mean response time. This finding
surprised us; we expected the beneficiary to gain far less from the
bursty help of a donor with irregular (highly variable) job sizes.
It seems intuitive that when donor job sizes are made more variable,
two things should happen. (i) The donor pain should drop. This is
because the donor mean response times will be higher overall, and so
the relative pain will appear diminished. (ii) The beneficiary gain
should drop. This is because high variability in the donor job sizes
implies high variability in the length of the donor busy periods,
which implies that the donor's visits to the beneficiary queue will
be more irregular. Sporadic help should be inferior to regular
help for the beneficiary.
Figure 6.6 shows that hypothesis (i)
is in fact true, while hypothesis (ii) is surprisingly false, at
least for  . Comparing Figure 6.5 row 1 (
. Comparing Figure 6.5 row 1 (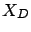 has low variability:
has low variability:
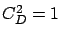 ) with Figure 6.6 (
) with Figure 6.6 (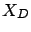 has high variability:
has high variability: 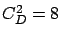 ), we
see that there is no discernible difference in beneficiary
performance.
), we
see that there is no discernible difference in beneficiary
performance.
To study this effect more closely, we next increase the variability in
donor job sizes further. Figure 6.7(a) shows the mean
response time of the beneficiary jobs when 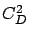 is 1, 8, or 50.
Figure 6.7(b) shows the ``impact'' of
is 1, 8, or 50.
Figure 6.7(b) shows the ``impact'' of 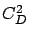 on the mean response time of the beneficiary jobs,
where the ``impact'' is defined to be the
mean response time of the beneficiary jobs when
on the mean response time of the beneficiary jobs,
where the ``impact'' is defined to be the
mean response time of the beneficiary jobs when 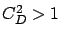 (specifically, two cases where
(specifically, two cases where 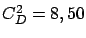 are shown) relative to
the mean response time of the beneficiary jobs when
are shown) relative to
the mean response time of the beneficiary jobs when 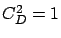 .
In Figure 6.7, switching times are set zero,
.
In Figure 6.7, switching times are set zero,
 is fixed at 0.5, and
is fixed at 0.5, and
 is varied from 0 to
is varied from 0 to 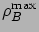 .
As observed in Figure 6.6, the effect of the variability of
.
As observed in Figure 6.6, the effect of the variability of 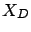 on
the mean response time of
on
the mean response time of  is small at
is small at  , and negligible
at
, and negligible
at 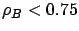 , when
, when 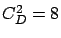 , although this effect increases
slightly when
, although this effect increases
slightly when 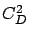 . When
. When 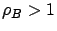 the effect of variability in
donor sizes can be significant. A critical factor seems to be whether
the beneficiary queue is stable in isolation; when this is not the
case, high variability in donor visits leads to prolonged intervals of
instability, which inflates the mean response time.
the effect of variability in
donor sizes can be significant. A critical factor seems to be whether
the beneficiary queue is stable in isolation; when this is not the
case, high variability in donor visits leads to prolonged intervals of
instability, which inflates the mean response time.
This is the same phenomenon seen in other related models studied by
Borst, Boxma and van Uitert [25] and by Borst,
Boxma and Jelenkovic [26] as well as in
Chapter 5. Borst, Boxma and van Uitert study the
coupled processor model, where two processors each serve their own
class of jobs, and if either is idle it may help the other, increasing
the rate of the other processor. This help incurs no switching time
and has a benefit even if only a single job is present (i.e. two
processors can work on the single job). They find that if a processor
has a load less than one, it is ``insulated'' from the heavy-tail of
the other, as long periods without cooperation will not lead to large
backlogs. This is not the case if the load is greater than one, as
the queue now must rely on help to be stable. Borst, Boxma and
Jelenkovic study the generalized processor sharing, where  classes
of jobs can share a processor with arbitrary weights. Using
probabilistic bounds, they show that different service rates can
either insulate the performance of different classes from the others
or not, again depending on whether the non-cooperative load is larger
than one.
classes
of jobs can share a processor with arbitrary weights. Using
probabilistic bounds, they show that different service rates can
either insulate the performance of different classes from the others
or not, again depending on whether the non-cooperative load is larger
than one.




Next: Effect of thresholds
Up: Mean response time
Previous: Benefit of cycle stealing:
Contents
Takayuki Osogami
2005-07-19
, variability of donor job sizes has very little effect on beneficiary mean response time.
![]() , we find variability of donor job sizes has very
little effect on beneficiary mean response time. This finding
surprised us; we expected the beneficiary to gain far less from the
bursty help of a donor with irregular (highly variable) job sizes.
, we find variability of donor job sizes has very
little effect on beneficiary mean response time. This finding
surprised us; we expected the beneficiary to gain far less from the
bursty help of a donor with irregular (highly variable) job sizes.
![]() . Comparing Figure 6.5 row 1 (
. Comparing Figure 6.5 row 1 (![]() has low variability:
has low variability:
![]() ) with Figure 6.6 (
) with Figure 6.6 (![]() has high variability:
has high variability: ![]() ), we
see that there is no discernible difference in beneficiary
performance.
), we
see that there is no discernible difference in beneficiary
performance.
![]() is 1, 8, or 50.
Figure 6.7(b) shows the ``impact'' of
is 1, 8, or 50.
Figure 6.7(b) shows the ``impact'' of ![]() on the mean response time of the beneficiary jobs,
where the ``impact'' is defined to be the
mean response time of the beneficiary jobs when
on the mean response time of the beneficiary jobs,
where the ``impact'' is defined to be the
mean response time of the beneficiary jobs when ![]() (specifically, two cases where
(specifically, two cases where ![]() are shown) relative to
the mean response time of the beneficiary jobs when
are shown) relative to
the mean response time of the beneficiary jobs when ![]() .
In Figure 6.7, switching times are set zero,
.
In Figure 6.7, switching times are set zero,
![]() is fixed at 0.5, and
is fixed at 0.5, and
![]() is varied from 0 to
is varied from 0 to ![]() .
As observed in Figure 6.6, the effect of the variability of
.
As observed in Figure 6.6, the effect of the variability of ![]() on
the mean response time of
on
the mean response time of ![]() is small at
is small at ![]() , and negligible
at
, and negligible
at ![]() , when
, when ![]() , although this effect increases
slightly when
, although this effect increases
slightly when ![]() . When
. When ![]() the effect of variability in
donor sizes can be significant. A critical factor seems to be whether
the beneficiary queue is stable in isolation; when this is not the
case, high variability in donor visits leads to prolonged intervals of
instability, which inflates the mean response time.
the effect of variability in
donor sizes can be significant. A critical factor seems to be whether
the beneficiary queue is stable in isolation; when this is not the
case, high variability in donor visits leads to prolonged intervals of
instability, which inflates the mean response time.
![]() classes
of jobs can share a processor with arbitrary weights. Using
probabilistic bounds, they show that different service rates can
either insulate the performance of different classes from the others
or not, again depending on whether the non-cooperative load is larger
than one.
classes
of jobs can share a processor with arbitrary weights. Using
probabilistic bounds, they show that different service rates can
either insulate the performance of different classes from the others
or not, again depending on whether the non-cooperative load is larger
than one.