



Next: Benefits of cycle stealing:
Up: Results
Previous: Stability
Contents
In this section, we study the mean response time of the beneficiary jobs
and the donor jobs, analyzed via DR.
Throughout we will use the term ``gain'' to denote the improvement
(drop) in mean response time experienced by beneficiary jobs under
cycle stealing, as compared with dedicated servers (without cycle stealing), and the
term ``pain'' to refer to the increase in mean response time
experienced by donor jobs under cycle stealing as compared with
dedicated servers:
where
![$\mbox{{\bf\sf E}}\left[ T_B \right]^{{\tt Dedicated}}$](img1449.png) refers to the mean response time of
beneficiary jobs under dedicated servers and
refers to the mean response time of
beneficiary jobs under dedicated servers and
![$\mbox{{\bf\sf E}}\left[ T_B \right]^{{\tt CS}}$](img1450.png) refers
to the mean response time of beneficiary jobs under cycle stealing.
refers
to the mean response time of beneficiary jobs under cycle stealing.
![$\mbox{{\bf\sf E}}\left[ T_D \right]^{{\tt Dedicated}}$](img1451.png) and
and
![$\mbox{{\bf\sf E}}\left[ T_D \right]^{{\tt CS}}$](img1452.png) are defined similarly.
Observe that both pain and gain have been defined to range from
are defined similarly.
Observe that both pain and gain have been defined to range from  to
to
 , where infinite gain corresponds to the situation where the
mean response time under dedicated is infinite while it is finite under
cycle stealing.
In Figures 6.4-6.7, we fix
the threshold values as
, where infinite gain corresponds to the situation where the
mean response time under dedicated is infinite while it is finite under
cycle stealing.
In Figures 6.4-6.7, we fix
the threshold values as
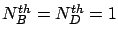 and
study the effect of other parameters, and
in Figures 6.8-6.9 we study the effect of the threshold values.
and
study the effect of other parameters, and
in Figures 6.8-6.9 we study the effect of the threshold values.
Subsections




Next: Benefits of cycle stealing:
Up: Results
Previous: Stability
Contents
Takayuki Osogami
2005-07-19
![\begin{displaymath}
\mbox{gain} = \frac{\mbox{{\bf\sf E}}\left[ T_B \right]^{{\t...
... CS}}}{\mbox{{\bf\sf E}}\left[ T_D \right]^{{\tt Dedicated}}},
\end{displaymath}](img1448.png)
![\begin{displaymath}
\mbox{gain} = \frac{\mbox{{\bf\sf E}}\left[ T_B \right]^{{\t...
... CS}}}{\mbox{{\bf\sf E}}\left[ T_D \right]^{{\tt Dedicated}}},
\end{displaymath}](img1448.png)