Dynamic robustness of threshold based policies

We have seen, in Section 7.3.2, that the mean response time of the optimized ADT policy is similar to that of the optimized T1 policy, although the ADT policy has greater static robustness. Note that this observation is based on the assumption of Poisson arrivals. Consider, to start, an alternate scenario, in which the load at queue 2 fluctuates. For example, a long high load period (e.g., $\rho_1=1.15$ and $\rho_2=0.8$) is followed by a long low load period (e.g., $\rho_1=1.15$ and $\rho_2=0.4$), and the high and low load periods alternate. The T1 policy with a fixed threshold value must have a high mean response time either during the high load period or during the low load period (recall Figure 7.6). On the other hand, the ADT policy may provide low mean response time during both high and low load periods, since the $T_1$ threshold value is self-adapted to the load (recall Figure 7.10). In this section, we study the mean response time of the ADT policy when the load fluctuates, or the dynamic robustness of the ADT policy.

We use a Markov modulated Poisson process of order two (MMPP(2)), as defined in Section 3.2, as an arrival process. An MMPP(2) has two types of periods, which we denote as the high load period and the low load period. The duration of each type of period has an exponential distribution, which can differ in each type of period. During the high (respectively, low) load period, the arrival process follows a Poisson process with rate $\lambda_H$ (respectively, $\lambda_L$), where $\lambda_H>\lambda_L$.

Figure 7.12: Dynamic robustness of the ADT policy and the T1 policy. The percentage change (%) in the mean response time of the (locally) optimized ADT policy over the optimized T1 policy for each given MMPP(2), shown as a function of the expected number of arrivals during a high load period, $\mbox{{\bf\sf E}}\left[ N_H \right]$, and during a low load period, $\mbox{{\bf\sf E}}\left[ N_L \right]$. A negative percentage indicates the improvement of ADT over T1. Here, $c_1=c_2=1$, $c_1\mu_1=c_1\mu_{12}=1$, and $\rho_1=1.15$ are fixed.

$\rho_2=[0.2,0.8]$

$\rho_2=[0.4,0.8]$

$\rho_2=[0.6,0.8]$

(a) $c_2\mu_2=\frac{1}{4}$

(b) $c_2\mu_2=\frac{1}{16}$

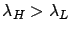Figure 7.12 shows the percentage change in the mean response time of the (locally) optimized ADT policy over the optimized T1 policy, when arrivals at queue 1 follow a Poisson process and arrivals at queue 2 follow an MMPP(2). The arrival rates in the MMPP(2) are chosen such that the load during the high load period is $\rho_2=0.8$ and the load during the low load period is $\rho_2=0.2$, 0.4, or 0.6, while $\rho_1=1.15$ is fixed throughout. Other parameter settings are the same as in Figure 7.11. We choose the horizontal axis to be the expected number of type 2 arrivals during a high load period, and the three lines (solid, dashed, and dotted) to be different expected number of type 2 arrivals during a low load period. Note that since there are less frequent arrivals during a low load period, having the same number of arrivals during the high and low load periods implies that the low load period is longer. Thus, the number of arrivals during each period is an indicator of how frequently the load changes, which we find to be an important parameter in studying dynamic robustness. The threshold values of the optimized T1 policy and the (locally) optimized ADT policy are chosen such that the overall weighted mean response time is minimized for each given arrival process.

The first thing to notice in Figure 7.12 is that the improvement of the ADT policy over the T1 policy is smaller when the duration of the high and low load periods is shorter, or equivalently when there are less arrivals in each period. This makes intuitive sense, since the MMPP(2) reduces to a Poisson process when the high and low load periods alternate infinitely quickly, and under the Poisson process, the optimized T1 policy and the optimized ADT policy provide similar mean response time (Section 7.3.2).

However, even when the durations are longer, the performance improvement of the ADT policy over the T1 policy is comparatively small (3 to 25%). This is mainly because the mean response time of the jobs arriving during the high load period tends to dominate the overall mean response time for two reasons: (i) the response time of jobs arriving during the high load period is much higher than that of jobs arriving during the low load period, partially due to the fact that any reasonable allocation policy (such as the optimized T1 policy and the optimized ADT policy) can provide low mean response time at low load, and (ii) assuming that a low load period and a high load period have the same duration, there are more arrivals during a high load period. Since the T1 policy with a fixed $T_1$ threshold can provide low mean response time for the jobs arriving during the high load period, it can provide low overall mean response time. (Of course, if there were many more arrivals during the low load period than the high load period, the $T_1$ threshold would be adjusted.)

It is only when the jobs arriving during the high load period and the jobs arriving during the low load period have roughly equal contribution to the overall mean response time ^7.1that the ADT policy can have appreciable improvement over the T1 policy. For example, Figure 7.12 suggests that the ADT policy can provide a mean response time that is 20-30% lower than that of the T1 policy, when the number of arrivals during a low load period is ($\sim 10$ times) larger than that during a high load period.

In addition (not shown), we find that when arrivals at queue 1 follow an MMPP(2) or when arrivals at both queues follow MMPP(2)'s, the improvement of the ADT policy over the T1 policy tends to be smaller than when only arrivals at queue 2 follow an MMPP(2). Overall, we conclude that the ADT policy has appreciable improvement over the T1 policy only when there are more arrivals during the low load period than during the high load period, giving them comparable importance.