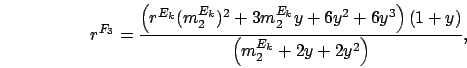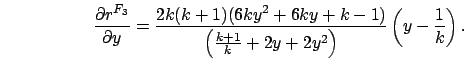Base case (![]() ):
Any one-phase PH distribution is a mixture of
):
Any one-phase PH distribution is a mixture of ![]() and an exponential distribution, and the
and an exponential distribution, and the ![]() -value is
always
-value is
always ![]() .
.
Inductive case:
Suppose that the lemma holds for ![]() .
We show that the lemma holds for
.
We show that the lemma holds for ![]() as well.
as well.
Consider any ![]() -phase acyclic PH distribution,
-phase acyclic PH distribution, ![]() , which is not an
Erlang distribution.
We first show that there exists a PH
distribution,
, which is not an
Erlang distribution.
We first show that there exists a PH
distribution, ![]() , with
, with
![]() such that
such that ![]() is the convolution of an exponential distribution,
is the convolution of an exponential distribution,
![]() , and a
, and a ![]() -phase PH distribution,
-phase PH distribution, ![]() .
The key idea is to see any PH
distribution as a mixture of
PH distributions whose initial probability vectors,
.
The key idea is to see any PH
distribution as a mixture of
PH distributions whose initial probability vectors, ![]() , are base vectors.
For example, the three-phase PH distribution,
, are base vectors.
For example, the three-phase PH distribution, ![]() , in Figure 2.1,
can be seen as a mixture of
, in Figure 2.1,
can be seen as a mixture of ![]() and the three 3-phase PH distribution,
and the three 3-phase PH distribution,
![]() (
(![]() ),
whose parameters are
),
whose parameters are
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
Proposition 5 and Lemma 2 imply that
there exists
.
Proposition 5 and Lemma 2 imply that
there exists
![]() such that
such that
![]() .
Without loss of generality, let
.
Without loss of generality, let
![]() and let
and let ![]() ;
thus,
;
thus,
![]() .
Note that
.
Note that
![]() is the convolution of an exponential distribution,
is the convolution of an exponential distribution,
![]() , and a
, and a ![]() -phase PH distribution,
-phase PH distribution, ![]() .
.
Next we show that if ![]() is not an Erlang distribution,
then there exists a PH
distribution,
is not an Erlang distribution,
then there exists a PH
distribution, ![]() , with no greater
, with no greater ![]() -value (i.e.
-value (i.e.
![]() ). Let
). Let ![]() be a mixture of
be a mixture of ![]() and an Erlang-
and an Erlang-![]() distribution,
distribution, ![]() , (i.e.
, (i.e.
![]() ), where
), where ![]() is chosen such that
is chosen such that
![]() and
and
![]() . There always
exists such a
. There always
exists such a ![]() , since the Erlang-
, since the Erlang-![]() distribution has the least
distribution has the least
![]() among all the PH distributions (in particular
among all the PH distributions (in particular
![]() ) and
) and ![]() is an increasing function of
is an increasing function of ![]() (
(
![]() ). Also, observe that, by Proposition 5 and the inductive
hypothesis,
). Also, observe that, by Proposition 5 and the inductive
hypothesis,
![]() .
Let
.
Let ![]() be the convolution of
be the convolution of ![]() and
and ![]() ,
i.e.
,
i.e.
![]() .
We prove that
.
We prove that
![]() .
Let
.
Let
![]() . Then,
. Then,
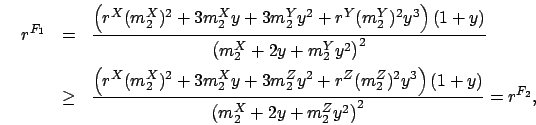
Finally, we show that an Erlang distribution has the least ![]() -value.
-value.
![]() is the convolution of
is the convolution of ![]() and
and ![]() , and it can also be seen as a mixture of
, and it can also be seen as a mixture of ![]() and a distribution,
and a distribution, ![]() ,
where
,
where
![]() .
Thus, by Lemma 2, at least one of
.
Thus, by Lemma 2, at least one of
![]() and
and
![]() holds.
When
holds.
When
![]() , the
, the ![]() -value of the Erlang-(
-value of the Erlang-(![]() ) distribution,
) distribution, ![]() ,
is smaller than
,
is smaller than ![]() , since
, since
![]() .
When
.
When
![]() (and hence
(and hence
![]() ),
),
![]() can be proved by showing
that
can be proved by showing
that ![]() is minimized when
is minimized when
![]() .
Let
.
Let
![]() .
Then,
.
Then,