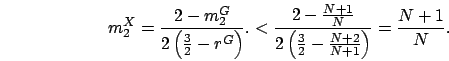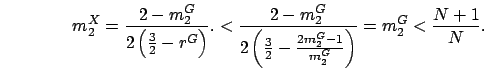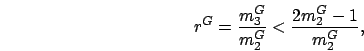Next: Proof of Lemma 6
Up: Proofs
Previous: Proof of Lemma 3
Contents
It is easy to check, by substitution, that conditions (2.10)-(2.12)
are satisfied.
It is easy to see  , since
, since
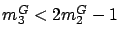 .
Also,
.
Also,
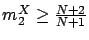 implies
implies 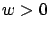 .
Thus, it suffices to prove that condition (2.9) is satisfied.
.
Thus, it suffices to prove that condition (2.9) is satisfied.
We first consider the first inequality of condition (2.9).
The assumption on 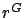 in the lemma gives
in the lemma gives
Therefore, since
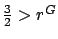 , it follows that
, it follows that
We next consider the second inequality of condition (2.9).
We begin by bounding the range of 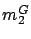 for
for  considered in the lemma.
Condition
considered in the lemma.
Condition
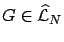 implies
implies
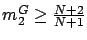 .
Also, if
.
Also, if 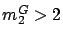 , then by the assumption on
, then by the assumption on 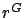 in lemma,
in lemma,
This contradicts
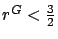 .
Thus,
.
Thus,  . So far, we derived the range of
. So far, we derived the range of 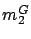 as
as
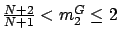 .
.
We prove
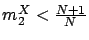 in two cases:
(i)
in two cases:
(i)
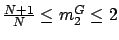 and (ii)
and (ii)
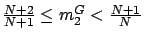 .
(i) When
.
(i) When
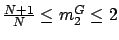 ,
,
The inequality follows from
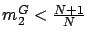 and
and
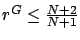 .
(ii) When
.
(ii) When
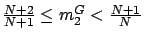 ,
,
The inequality follows from
which follows from
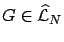 .
width 1ex height 1ex depth 0pt
.
width 1ex height 1ex depth 0pt




Next: Proof of Lemma 6
Up: Proofs
Previous: Proof of Lemma 3
Contents
Takayuki Osogami
2005-07-19
![]() in the lemma gives
in the lemma gives

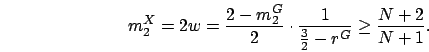
![]() for
for ![]() considered in the lemma.
Condition
considered in the lemma.
Condition
![]() implies
implies
![]() .
Also, if
.
Also, if ![]() , then by the assumption on
, then by the assumption on ![]() in lemma,
in lemma,
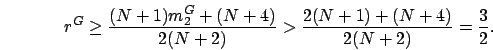
![]() in two cases:
(i)
in two cases:
(i)
![]() and (ii)
and (ii)
![]() .
(i) When
.
(i) When
![]() ,
,