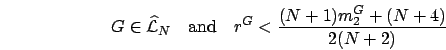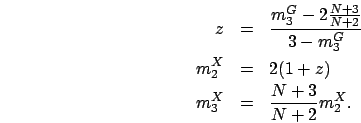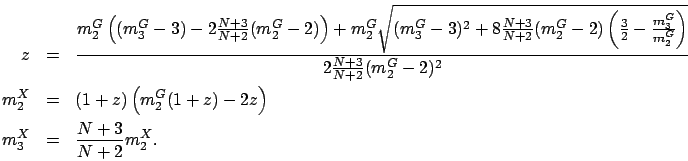Next: Analyzing the number of
Up: Positive closed form solution
Previous: Positive closed form solution
Contents
Figure 2.15:
An implementation of the Positive solution,
defined for a distribution
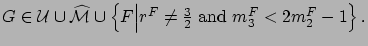
![\begin{figure}\begin{center}
\begin{tabular}[hbt]{\vert l\vert}\hline
($n$, $p$,...
...\mu_1^X$, $\mu_2^X$, $\mu_3^X$)\\
\hline
\end{tabular}
\end{center}\end{figure}](img427.png) |
The Positive solution is defined for almost all the input distributions in  .
Specifically, it is defined for all the distributions in
.
Specifically, it is defined for all the distributions in
Figure 2.15 shows an implementation of the Positive solution.
Below, we elaborate on the Positive solution, and prove an upper bound
on the number of phases used in the Positive solution.
When the input distribution  is in
is in
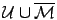 ,
the EC distribution produced by the Minimal solution does not have a mass probability at zero.
When
,
the EC distribution produced by the Minimal solution does not have a mass probability at zero.
When  is in
is in
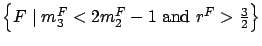 ,
,
 can be well-represented by a two-phase Coxian
can be well-represented by a two-phase Coxian PH distribution,
whose parameters are given by (2.4)-(2.5).
Below, we focus on input distributions
PH distribution,
whose parameters are given by (2.4)-(2.5).
Below, we focus on input distributions
 .
.
We first consider the first approach of using a mixture of an EC distribution
(with no mass probability at zero),  , and an exponential distribution,
, and an exponential distribution,  ,
(i.e.
,
(i.e.
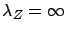 ).
Let
).
Let
Given a distribution
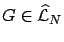 ,
we seek
,
we seek 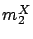 ,
, 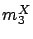 ,
,  , and
, and  such that
such that
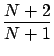 |
 |
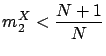 |
(2.9) |
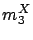 |
 |
 |
(2.10) |
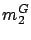 |
 |
 |
(2.11) |
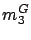 |
 |
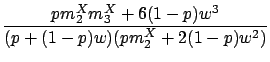 |
(2.12) |
Note that (2.9)-(2.10) guarantee that
we can find, via the Complete solution, an (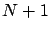 )-phase EC distribution,
)-phase EC distribution,  ,
such that
,
such that  has no mass probability at zero and has normalized moments
has no mass probability at zero and has normalized moments 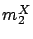 and
and 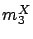 .
Let
.
Let  be the exponential distribution with
be the exponential distribution with
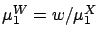 .
(2.11)-(2.12) guarantee that,
by choosing
.
(2.11)-(2.12) guarantee that,
by choosing 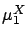 appropriately,
appropriately,
 is well-represented by a distribution
is well-represented by a distribution  , where
, where
The following lemma provides conditions on the input distribution
for which the first approach is defined.
Lemma 5
Suppose
for 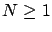 (see Figure 2.16(a)).
Let
Then,
(see Figure 2.16(a)).
Let
Then, 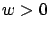 ,
,  , and
conditions (2.9)-(2.12) are satisfied.
, and
conditions (2.9)-(2.12) are satisfied.
A proof of Lemma 5 is postponed to Appendix A.
Figure 2.16:
Two regions in 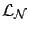 that input
that input  can fall into under the Positive solution:
(a)
can fall into under the Positive solution:
(a)  is well-represented by a mixture of an EC distribution
is well-represented by a mixture of an EC distribution  and an exponential distribution
and an exponential distribution  ;
(b)
;
(b)  is well-represented by the convolution of an EC distribution
is well-represented by the convolution of an EC distribution  and an exponential distribution
and an exponential distribution  .
.
|
|
The key idea behind Lemma 5 is to fix some of the
parameters so that the set of equations becomes simpler and yet there
exists a unique solution. The difficulty in finding closed form
solutions is that we are given a system of nonlinear equations with
high degree (2.10)-(2.12), and the solutions are not unique. By fixing some of the
parameters, the system of equations can be reduced to have a unique
solution. We find
that 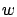 given by Lemma 5 has nice characteristics. First,
given by Lemma 5 has nice characteristics. First,
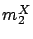 leads to a very simple expression:
leads to a very simple expression: 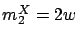 .
Second, with this expression of
.
Second, with this expression of 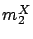 ,
the expression involving
,
the expression involving 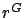 is significantly simplified:
is significantly simplified:
Now, solving (2.10)-(2.12) for  and
and 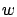 is a relatively easy task,
and
is a relatively easy task,
and  and
and 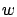 immediately gives
immediately gives 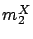 and
and 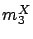 . Although
Lemma 5 allows us to find a simple closed form
solution, the set of input distributions defined for
Lemma 5 is rather small. This necessitates the
second approach of using the convolution of an EC distribution and an
exponential distribution. Note that the second approach alone does
not suffice, either. Applying the first approach to a small set of
input distributions and applying the second approach to the rest of
the input distribution, in fact, lead to simpler
closed form solutions by both approaches.
. Although
Lemma 5 allows us to find a simple closed form
solution, the set of input distributions defined for
Lemma 5 is rather small. This necessitates the
second approach of using the convolution of an EC distribution and an
exponential distribution. Note that the second approach alone does
not suffice, either. Applying the first approach to a small set of
input distributions and applying the second approach to the rest of
the input distribution, in fact, lead to simpler
closed form solutions by both approaches.
Next, we consider the second approach of using the convolution of an EC distribution
(with mass probability at zero) and an exponential distribution
(i.e.
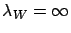 ).
Given a distribution
).
Given a distribution
 (we assume
(we assume
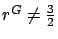 ),
we seek
),
we seek 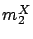 ,
, 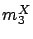 , and
, and 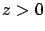 such that
such that
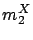 |
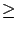 |
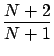 |
(2.13) |
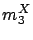 |
 |
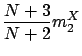 |
(2.14) |
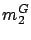 |
 |
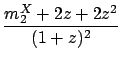 |
(2.15) |
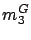 |
 |
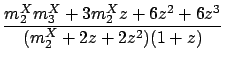 |
(2.16) |
Note that (2.13)-(2.14) guarantees that
we can find, via the Complete solution, an (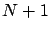 )-phase EC distribution,
)-phase EC distribution,  ,
such that
,
such that  has no mass probability at zero and has normalized moments
has no mass probability at zero and has normalized moments 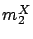 and
and 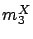 .
Let
.
Let  be the exponential distribution whose first moment is
be the exponential distribution whose first moment is
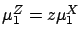 , where
, where 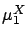 is the first moment of
is the first moment of  .
(2.15)-(2.16) guarantee that,
by choosing
.
(2.15)-(2.16) guarantee that,
by choosing 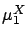 appropriately,
appropriately,
 is well-represented by the convolution of
is well-represented by the convolution of  and
and  .
.
The following lemma provides conditions on the input distribution
for which the second approach is defined.
Lemma 6
Suppose
for 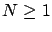 (see Figure 2.16(b)).
If
(see Figure 2.16(b)).
If 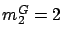 , we choose
If
, we choose
If 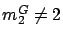 , we choose
Then,
, we choose
Then, 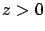 and
conditions (2.13)-(2.16) are satisfied.
and
conditions (2.13)-(2.16) are satisfied.
A proof of Lemma 6 is postponed to Appendix A.




Next: Analyzing the number of
Up: Positive closed form solution
Previous: Positive closed form solution
Contents
Takayuki Osogami
2005-07-19
![\begin{figure}\begin{center}
\begin{tabular}[hbt]{\vert l\vert}\hline
($n$, $p$,...
...\mu_1^X$, $\mu_2^X$, $\mu_3^X$)\\
\hline
\end{tabular}
\end{center}\end{figure}](img427.png)
![]() .
Specifically, it is defined for all the distributions in
.
Specifically, it is defined for all the distributions in
![]() is in
is in
![]() ,
the EC distribution produced by the Minimal solution does not have a mass probability at zero.
When
,
the EC distribution produced by the Minimal solution does not have a mass probability at zero.
When ![]() is in
is in
![]() ,
,
![]() can be well-represented by a two-phase Coxian
can be well-represented by a two-phase Coxian![]() PH distribution,
whose parameters are given by (2.4)-(2.5).
Below, we focus on input distributions
PH distribution,
whose parameters are given by (2.4)-(2.5).
Below, we focus on input distributions
![]() .
.
![]() , and an exponential distribution,
, and an exponential distribution, ![]() ,
(i.e.
,
(i.e.
![]() ).
Let
).
Let
![]() given by Lemma 5 has nice characteristics. First,
given by Lemma 5 has nice characteristics. First,
![]() leads to a very simple expression:
leads to a very simple expression: ![]() .
Second, with this expression of
.
Second, with this expression of ![]() ,
the expression involving
,
the expression involving ![]() is significantly simplified:
is significantly simplified:

![]() ).
Given a distribution
).
Given a distribution
![]() (we assume
(we assume
![]() ),
we seek
),
we seek ![]() ,
, ![]() , and
, and ![]() such that
such that