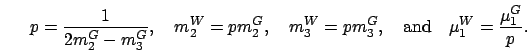Next: Analyzing the number of
Up: Simple closed form solution
Previous: Preliminaries
Contents
We are now ready to present the Simple solution. The Simple solution assumes that
 , where
, where
 . Observe
. Observe
 includes
almost all distributions in
includes
almost all distributions in  . Only the borders between
the
. Only the borders between
the  's,
's, 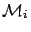 's, and
's, and 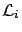 's are not included.
Figure 2.11 shows an implementation of the Simple solution.
The solution differs according to the classification of the input
distribution
's are not included.
Figure 2.11 shows an implementation of the Simple solution.
The solution differs according to the classification of the input
distribution  .
When
.
When
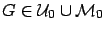 ,
a two-phase
Coxian
,
a two-phase
Coxian PH distribution suffices to match the first three moments. When
PH distribution suffices to match the first three moments. When
 ,
,
 is well-represented by an EC
distribution with
is well-represented by an EC
distribution with 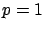 . When
. When
 ,
,
 is well-represented by an EC distribution with
is well-represented by an EC distribution with  .
.
Figure 2.12:
Ideas in the Simple solution.
Let  be the input distribution.
(i) If
be the input distribution.
(i) If
 ,
,  is well-represented by a two-phase Coxian
is well-represented by a two-phase Coxian PH distribution
PH distribution  .
(ii) If
.
(ii) If
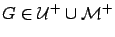 ,
,  is well-represented by
is well-represented by 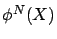 , where
, where  is a two-phase Coxian
is a two-phase Coxian PH distribution.
(iii) If
PH distribution.
(iii) If
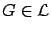 ,
,  is well-represented by
is well-represented by 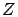 , where
, where  has a distribution function
has a distribution function
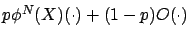 .
.
|
|
(i) If
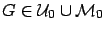 (see Figure 2.12(i)),
then a two-phase
Coxian
(see Figure 2.12(i)),
then a two-phase
Coxian PH distribution suffices to match the first three moments, i.e.,
PH distribution suffices to match the first three moments, i.e., 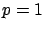 and
and  (
(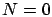 ). The parameters
(
). The parameters
( ,
,  ,
,  )
of the two-phase Coxian
)
of the two-phase Coxian PH distribution are chosen as follows [144,190]:
PH distribution are chosen as follows [144,190]:
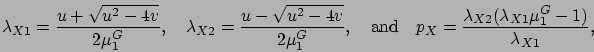 |
(2.4) |
where
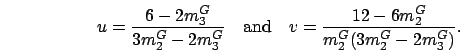 |
(2.5) |
(ii) If
 (see Figure 2.12(ii)),
Corollary 1 specifies the number of phases needed:
(see Figure 2.12(ii)),
Corollary 1 specifies the number of phases needed:
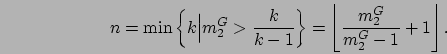 |
(2.6) |
Let 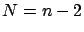 .
Next, we find the two-phase Coxian
.
Next, we find the two-phase Coxian PH distribution
PH distribution
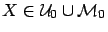 such that
such that  is well-represented by
is well-represented by
 .
By Theorem 3, this can be achieved by setting
.
By Theorem 3, this can be achieved by setting
where
Thus, we set 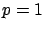 , and the parameters
(
, and the parameters
( ,
,  ,
,  ) of
) of  are given by case (i),
using
are given by case (i),
using 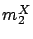 ,
, 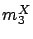 , and
, and 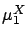 , specified above.
, specified above.
(iii) If  (see Figure 2.12(iii)),
then let
(see Figure 2.12(iii)),
then let
Observe that  satisfies
satisfies 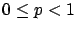 .
Also, since
.
Also, since  is in
is in 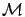 ,
,  can be chosen as an EC distribution with no mass probability at zero.
If
can be chosen as an EC distribution with no mass probability at zero.
If
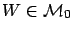 , the parameters of
, the parameters of  are provided by case (i), using
are provided by case (i), using  ,
,  , and
, and  , specified above.
If
, specified above.
If
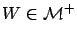 , the parameters of
, the parameters of  are provided by case (ii), using
are provided by case (ii), using  ,
,  , and
, and  , specified above.
, specified above.
 is then well-represented by distribution
is then well-represented by distribution  ,
where
,
where
 .
.




Next: Analyzing the number of
Up: Simple closed form solution
Previous: Preliminaries
Contents
Takayuki Osogami
2005-07-19
![]() , where
, where
![]() . Observe
. Observe
![]() includes
almost all distributions in
includes
almost all distributions in ![]() . Only the borders between
the
. Only the borders between
the ![]() 's,
's, ![]() 's, and
's, and ![]() 's are not included.
Figure 2.11 shows an implementation of the Simple solution.
The solution differs according to the classification of the input
distribution
's are not included.
Figure 2.11 shows an implementation of the Simple solution.
The solution differs according to the classification of the input
distribution ![]() .
When
.
When
![]() ,
a two-phase
Coxian
,
a two-phase
Coxian![]() PH distribution suffices to match the first three moments. When
PH distribution suffices to match the first three moments. When
![]() ,
,
![]() is well-represented by an EC
distribution with
is well-represented by an EC
distribution with ![]() . When
. When
![]() ,
,
![]() is well-represented by an EC distribution with
is well-represented by an EC distribution with ![]() .
.
![]() (see Figure 2.12(i)),
then a two-phase
Coxian
(see Figure 2.12(i)),
then a two-phase
Coxian![]() PH distribution suffices to match the first three moments, i.e.,
PH distribution suffices to match the first three moments, i.e., ![]() and
and ![]() (
(![]() ). The parameters
(
). The parameters
(![]() ,
, ![]() ,
, ![]() )
of the two-phase Coxian
)
of the two-phase Coxian![]() PH distribution are chosen as follows [144,190]:
PH distribution are chosen as follows [144,190]:
![]() (see Figure 2.12(ii)),
Corollary 1 specifies the number of phases needed:
(see Figure 2.12(ii)),
Corollary 1 specifies the number of phases needed:
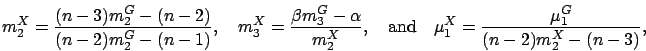
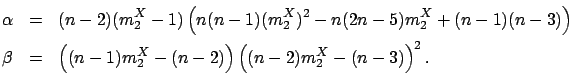
![]() (see Figure 2.12(iii)),
then let
(see Figure 2.12(iii)),
then let