next up previous contents
Next: The Simple solution Up: Simple closed form solution Previous: Simple closed form solution   Contents

Preliminaries

Figure 2.10: A classification of distributions. The dotted lines delineate the set of all nonnegative distributions $G$ ( $m_3^G \geq m_2^G \geq 1$).
\includegraphics[width=0.35\linewidth]{fig/region2.eps}

Set ${\cal T}^{(n)}$, which is used to characterize set ${\cal S}^{(n)}$, gives us a sense of how many phases are necessary to well-represent a given distribution. It turns out that it is useful to divide set ${\cal T}^{(n)}$ into smaller subsets to describe the closed form solutions compactly. Roughly speaking, we divide the set ${\cal T}^{(n)} \setminus {\cal T}^{(n-1)}$ into three subsets, ${\cal U}_{n-1}$, ${\cal M}_{n-1}$, and ${\cal L}_{n-1}$ (see Figure 2.10). More formally,

Definition 13   We define ${\cal U}_i$, ${\cal M}_i$, and ${\cal L}_i$ as follows:

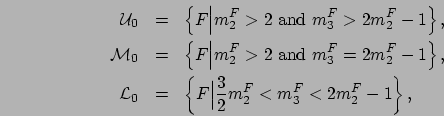
\begin{eqnarray*} {\cal U}_0 & = & \left\{ F \Big\vert m_2^F > 2 \mbox{ and } m_... ...eft\{ F \Big\vert \frac{3}{2}m_2^F < m_3^F < 2m_2^F - 1\right\}, \end{eqnarray*}

and

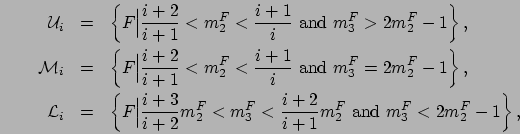
\begin{eqnarray*} {\cal U}_i & = & \left\{ F \Big\vert \frac{i+2}{i+1} < m_2^F <... ... < \frac{i+2}{i+1}m_2^F \mbox{ and } m_3^F < 2m_2^F - 1\right\}, \end{eqnarray*}

for nonnegative integers $i$. Also, let ${\cal U}^+=\cup_{i=1}^\infty {\cal U}_i$, ${\cal M}^+=\cup_{i=1}^\infty {\cal M}_i$, ${\cal L}^+=\cup_{i=1}^\infty {\cal L}_i$, ${\cal U}={\cal U}_0\cup {\cal U}^+$, ${\cal M}={\cal M}_0\cup {\cal M}^+$, and ${\cal L}={\cal L}_0\cup {\cal L}^+$. Further, let

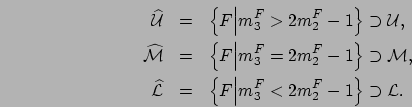
\begin{eqnarray*} \widehat{\cal U} & = & \left\{ F \Big\vert m_3^F > 2m_2^F - 1\... ... \left\{ F \Big\vert m_3^F < 2m_2^F - 1\right\} \supset \cal{L}. \end{eqnarray*}

Observe that $\widehat{\cal U}$ includes both $\cal{U}$ and borders between ${\cal U}_i$ and ${\cal U}_{i+1}$, for $i\geq 0$, that are not included in $\cal{U}$.

The sets $\widehat{\cal U}$, $\widehat{\cal M}$, and $\widehat{\cal L}$ provide a classification of distributions into three categories such that, for any distribution ${X}$, ${X}$ and $\phi({X})$ lie in the same category.

Lemma 4   Let ${Z_N}=\phi^N({X})$ for integers $N\geq 1$. If ${X}\in \widehat{\cal U}$ (respectively, ${X}\in \widehat{\cal M}$, ${X}\in \widehat{\cal L}$), then ${Z_N}\in \widehat{\cal U}$ (respectively, ${Z_N}\in \widehat{\cal M}$, ${Z_N}\in \widehat{\cal L}$).


Proof:We prove the case when $N=1$. The lemma then follows by induction. Let ${Z}=\phi({X})$. By Theorem 3, $m_2^{X} = 1 / (2-m_2^{Z})$, and

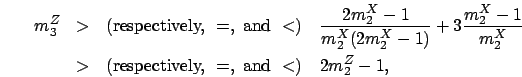
\begin{eqnarray*} m_3^{Z} & > & (\mbox{respectively, } =,\mbox{ and } <)\quad ... ... > & (\mbox{respectively, } =,\mbox{ and } <)\quad 2m_2^{Z} - 1, \end{eqnarray*}

where the last equality follows from $m_2^{X} = 1 / (2-m_2^{Z})$.     width 1ex height 1ex depth 0pt

By Corollary 1 and Lemma 4, it follows that:

Corollary 2   Let ${Z_N}=\phi^N({X})$ for $N\geq 0$. If ${X}\in {\cal U}_0$ (respectively, ${X}\in {\cal M}_0$), then ${Z_N}\in {\cal U}_N$ (respectively, ${Z_N}\in {\cal M}_N$).

The corollary implies that for any $G\in {\cal U}_N\cup {\cal M}_N$, $G$ can be well-represented by an $(N+2)$-phase EC distribution with no mass probability at zero ($p=1$), because, for any $X\in {\cal U}_0\cup {\cal M}_0$, $X$ can be well-represented by a two-phase Coxian$^+$ PH distribution, and hence ${Z_N}=\phi^N({X})$ can be well-represented by an $(N+2)$-phase EC distribution. (Recall $\cal{U}_N,\cal{M}_N,\cal{L}_N\subset \cal{T}_{N+1}$.) Below, it will also be shown that for any $G\in {\cal L}_N$, $G$ can be well-represented by an $(N+2)$-phase EC distribution with positive mass probability at zero ($p<1$).

By Corollary 2, it is relatively easy to provide a closed form solution for the parameters ($n$, $p$, $\lambda_{X1}$, $\lambda_{X2}$, $p_X$) of an EC distribution, $Z$, so that a given distribution is well-represented by $Z$. Essentially, one just needs to find an appropriate $N$ and solve $Z=\phi^N(X)$ for $X$ in terms of normalized moments, which is immediate since $N$ is given by Corollary 1 and the normalized moments of $X$ can be obtained from Theorem 3.

Figure 2.11: An implementation of the Simple solution, defined for $G\in {\cal PH}_3^- \equiv {\cal U} \cup {\cal M} \cup {\cal L}$.
\begin{figure}\begin{center} \begin{tabular}[hbt]{\vert l\vert}\hline ($n$, $p$,... ...\frac{1}{(m_2^{X}-1)\mu_1^{X}}$.\\ \hline \end{tabular} \end{center}\end{figure}

next up previous contents
Next: The Simple solution Up: Simple closed form solution Previous: Simple closed form solution   Contents
Takayuki Osogami 2005-07-19