Positive closed form solution

The Positive solution is built upon the Complete solution, but does not have mass probability at zero. The key idea in the design of the Positive solution is to match the input distribution either by a mixture of an EC distribution (with no mass probability at zero) and an exponential distribution, or by the convolution of an EC distribution (with positive mass probability at zero) and an exponential distribution. The use of these types of distributions makes intuitive sense, since they can approximate the EC distribution with mass probability at zero arbitrarily closely by letting the rate of the exponential distributions approach infinity. Therefore, in this section, we extend the definition of the EC distribution and use the extended EC distribution to well-represent the input distribution.

Definition 14   An extended EC distribution has a distribution function either of the form 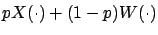$pX(\cdot)+(1-p)W(\cdot)$ or of the form 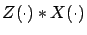$Z(\cdot)\ast X(\cdot)$, where $X$ is an EC distribution with no mass probability at zero; $Z$ and $W$ are exponential distributions.

See Figure 2.3 for the Markov chain whose absorption time defines an extended EC distribution. Note that the parameter $n$ in an extended EC distribution denotes the number of phases in the EC portion of the extended EC distribution. Therefore, the total number of phases in the extended EC distribution is $n+1$.