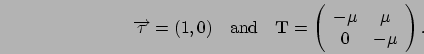We start by providing canonical examples of QBD processes. Here, we provide both pictorial explanation and more formal explanation. Pictorial explanation gives intuitive understanding of the QBD process, and more formal explanation allows us to get used to the notation that we use later.
First, a birth-and-death process is an example of a QBD process.
Figure 3.8(a) shows an example of a birth-and-death
process. This birth-and-death process models the number of jobs in an
M/M/1 queue, where jobs arrive according to a Poisson process with
rate ![]() , and the service demand has an exponential distribution
with rate
, and the service demand has an exponential distribution
with rate ![]() . In general, a birth-and-death process is a Markov
chain on the states
. In general, a birth-and-death process is a Markov
chain on the states
![]() , where transitions are allowed only to the neighboring states. That
is, from state
, where transitions are allowed only to the neighboring states. That
is, from state ![]() , there are transitions only to state
, there are transitions only to state ![]() and state
and state ![]() for
for ![]() , and from state 0, there is a
transition only to state 1. Thus, the generator matrix of a
birth-and-death process is of the form:
, and from state 0, there is a
transition only to state 1. Thus, the generator matrix of a
birth-and-death process is of the form:
Figure 3.8(b) shows an example of a QBD process
that is not a birth-and-death process.
This QBD process models the number of jobs in a M/Er/1 queue,
where jobs arrive according to a Poisson process with rate ![]() ,
and their service demand has an Erlang-2 distribution (as defined in Section 2.2),
which has parameters
,
and their service demand has an Erlang-2 distribution (as defined in Section 2.2),
which has parameters