


Next: Active Learning with
Up: Locally Weighted Regression
Previous: Locally Weighted Regression
There are a number of ways one can set k, the smoothing parameter.
The method used by Cleveland
et al. [1988] is to set
k such that the reference point being predicted has a predetermined
amount of support, that is, k is set so that n is close to some
target value. This has the disadvantage of requiring assumptions about
the noise and smoothness of the function being learned. Another
technique, used by Schaal and
Atkeson [1994]
sets k to minimize the crossvalidated error on the training set. A
disadvantage of this technique is that it assumes the distribution of
the training set is representative of 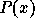 , which it may not be in
an active learning situation. A third method, also described by Schaal and
Atkeson [1994], is to set k so as to
minimize the estimate of
, which it may not be in
an active learning situation. A third method, also described by Schaal and
Atkeson [1994], is to set k so as to
minimize the estimate of 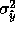 at the reference
points. As k decreases, the regression becomes more global. The
total weight n will increase (which decreases
at the reference
points. As k decreases, the regression becomes more global. The
total weight n will increase (which decreases 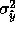 ),
but so will the conditional variance
),
but so will the conditional variance 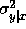 (which increases
(which increases
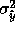 ). At some value of k, these two quantities
will balance to produce a minimum estimated variance (see
Figure 3). This estimate can be computed for arbitrary
reference points in the domain, and the user has the option of using
either a different k for each reference point or a single global k
that minimizes the average
). At some value of k, these two quantities
will balance to produce a minimum estimated variance (see
Figure 3). This estimate can be computed for arbitrary
reference points in the domain, and the user has the option of using
either a different k for each reference point or a single global k
that minimizes the average 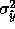 over all reference
points. Empirically, we found that the variance-based method gave the
best performance.
over all reference
points. Empirically, we found that the variance-based method gave the
best performance.
David Cohn
Mon Mar 25 09:20:31 EST 1996
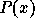 , which it may not be in
an active learning situation. A third method, also described by Schaal and
Atkeson [1994], is to set k so as to
minimize the estimate of
, which it may not be in
an active learning situation. A third method, also described by Schaal and
Atkeson [1994], is to set k so as to
minimize the estimate of 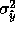 at the reference
points. As k decreases, the regression becomes more global. The
total weight n will increase (which decreases
at the reference
points. As k decreases, the regression becomes more global. The
total weight n will increase (which decreases 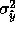 ),
but so will the conditional variance
),
but so will the conditional variance 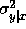 (which increases
(which increases
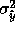 ). At some value of k, these two quantities
will balance to produce a minimum estimated variance (see
Figure 3). This estimate can be computed for arbitrary
reference points in the domain, and the user has the option of using
either a different k for each reference point or a single global k
that minimizes the average
). At some value of k, these two quantities
will balance to produce a minimum estimated variance (see
Figure 3). This estimate can be computed for arbitrary
reference points in the domain, and the user has the option of using
either a different k for each reference point or a single global k
that minimizes the average 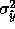 over all reference
points. Empirically, we found that the variance-based method gave the
best performance.
over all reference
points. Empirically, we found that the variance-based method gave the
best performance.


