
Figure 2: In locally weighted regression, points are weighted by proximity to the current x in question using a kernel. A regression is then computed using the weighted points.



Model-based methods, such as neural networks and the mixture of Gaussians, use the data to build a parameterized model. After training, the model is used for predictions and the data are generally discarded. In contrast, ``memory-based'' methods are non-parametric approaches that explicitly retain the training data, and use it each time a prediction needs to be made. Locally weighted regression (LWR) is a memory-based method that performs a regression around a point of interest using only training data that are ``local'' to that point. One recent study demonstrated that LWR was suitable for real-time control by constructing an LWR-based system that learned a difficult juggling task [Schaal & Atkeson 1994].

Figure 2:
In locally weighted regression, points are weighted by proximity to
the current x in question using a kernel. A regression is then
computed using the weighted points.
We consider here a form of locally weighted regression that is a variant of the LOESS model [Cleveland et al. 1988]. The LOESS model performs a linear regression on points in the data set, weighted by a kernel centered at x (see Figure 2). The kernel shape is a design parameter for which there are many possible choices: the original LOESS model uses a ``tricubic'' kernel; in our experiments we have used a Gaussian
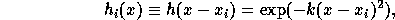
where k is a smoothing parameter. In Section 4.1 we will describe several methods for automatically setting k.
For brevity, we will drop the argument x for 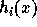 , and define
, and define 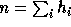 . We can then write the estimated means and covariances
as:
. We can then write the estimated means and covariances
as:

We use the data covariances to express the conditional expectations and their estimated variances:
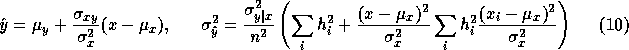
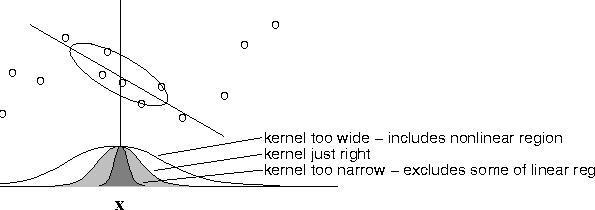
Figure 3:
The estimator variance is minimized when the kernel includes as many
training points as can be accommodated by the model. Here the linear
LOESS model is shown. Too large a kernel includes points that degrade
the fit; too small a kernel neglects points that increase confidence
in the fit.


