


Next: Experimental Results
Up: Locally Weighted Regression
Previous: Setting the Smoothing
As with the mixture of Gaussians, we want to select  to
minimize
to
minimize  . To do this, we
must estimate the mean and variance of
. To do this, we
must estimate the mean and variance of 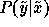 . With
locally weighted regression, these are explicit: the mean is
. With
locally weighted regression, these are explicit: the mean is
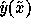 and the variance is
and the variance is 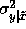 .
The estimate of
.
The estimate of  is also
explicit. Defining
is also
explicit. Defining  as the weight assigned to
as the weight assigned to  by the kernel we can compute these expectations exactly in closed form.
For the LOESS model, the learner's expected new variance is
by the kernel we can compute these expectations exactly in closed form.
For the LOESS model, the learner's expected new variance is

Note that, since  , the new expectation of
Equation 11 may be efficiently computed by caching the
values of
, the new expectation of
Equation 11 may be efficiently computed by caching the
values of  and
and  . This obviates
the need to recompute the entire sum for each new candidate point.
The component expectations in Equation 11 are computed as
follows:
. This obviates
the need to recompute the entire sum for each new candidate point.
The component expectations in Equation 11 are computed as
follows:

Just as with the mixture of Gaussians, we can use the expectation in
Equation 11 to guide active learning.
David Cohn
Mon Mar 25 09:20:31 EST 1996
 to
minimize
to
minimize  . To do this, we
must estimate the mean and variance of
. To do this, we
must estimate the mean and variance of 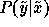 . With
locally weighted regression, these are explicit: the mean is
. With
locally weighted regression, these are explicit: the mean is
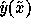 and the variance is
and the variance is 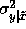 .
The estimate of
.
The estimate of  is also
explicit. Defining
is also
explicit. Defining  as the weight assigned to
as the weight assigned to  by the kernel we can compute these expectations exactly in closed form.
For the LOESS model, the learner's expected new variance is
by the kernel we can compute these expectations exactly in closed form.
For the LOESS model, the learner's expected new variance is




 , the new expectation of
Equation
, the new expectation of
Equation  and
and  . This obviates
the need to recompute the entire sum for each new candidate point.
The component expectations in Equation
. This obviates
the need to recompute the entire sum for each new candidate point.
The component expectations in Equation 