


Next: O-contract Paths - Monotone
Up: Lower Bounds on Path Length
Previous: Overview
 -contract Paths - Unrestricted Utility Functions
-contract Paths - Unrestricted Utility Functions
Our first result clarifies one issue in the presentation of [Sandholm, 1998, Proposition 2]: in this
an upper bound that is exponential in  is proved on the length of IR
is proved on the length of IR  -contract paths, i.e.
in terms of our notation, [Sandholm, 1998, Proposition 2] establishes an upper bound on
-contract paths, i.e.
in terms of our notation, [Sandholm, 1998, Proposition 2] establishes an upper bound on
 . We now prove a similar order lower bound.
. We now prove a similar order lower bound.
Theorem 3
Let

be the predicate which holds whenever

is an IR

-contract and

that which holds whenever

is IR. For
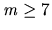
Proof. Consider a path
 in
in
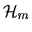 ,
with the following property4
,
with the following property4
e.g. if  then
then
is such a path as it corresponds to the sequence
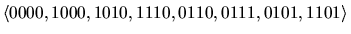 .
.
Choose
 to be a longest such path with this property that could be formed
in
to be a longest such path with this property that could be formed
in
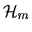 , letting
, letting
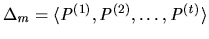 be the sequence of allocations
with
be the sequence of allocations
with
 .
We now define the utility functions
.
We now define the utility functions  and
and  so that for
so that for
 ,
,
With this choice, the contract path  describes the unique IR
describes the unique IR  -contract path
realising the IR deal
-contract path
realising the IR deal
 : that
: that
 is an IR
is an IR  -contract path is immediate, since
-contract path is immediate, since
That it is unique follows from the fact that for all  and
and
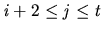 , the deal
, the deal
 is not an
is not an  -contract
(hence there are no ``short-cuts'' possible), and for each
-contract
(hence there are no ``short-cuts'' possible), and for each  there is
exactly one IR
there is
exactly one IR  -contract that can follow it,
i.e.
-contract that can follow it,
i.e. 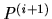 .5
.5
From the preceding argument it follows that any lower bound on the length of
 , i.e. a
sequence satisfying the condition (SC), is a lower bound on
, i.e. a
sequence satisfying the condition (SC), is a lower bound on
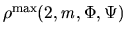 .
These paths in
.
These paths in
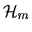 were originally
studied in [Kautz, 1958] in the context of coding theory and the lower bound
on their length of
were originally
studied in [Kautz, 1958] in the context of coding theory and the lower bound
on their length of 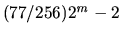 established in [Abbott & Katchalski, 1991].
established in [Abbott & Katchalski, 1991].
Example 1
Using the path
in the resource allocation setting
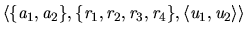
, if the
utility functions are specified as in Table
1 below then
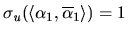
and
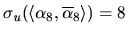
.
Furthermore,
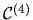
describes the unique IR

-contract path realising the reallocation
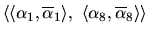
Table 1:
Utility function definitions for  example.
example.
|
|
There are a number of alternative formulations of ``rationality'' which can also be considered.
For example
There are a number of views we can take concerning the rationality conditions
given in Definition 7. One shared feature is that, unlike the concept of
individual rationality for which some provision to compensate agents who suffer a loss in utility
is needed, i.e. individual rationality presumes a ``money-based'' system, the forms defined
in Definition 7 allow concepts of ``rationality'' to be given in ``money-free''
enviroments. Thus, in a cooperatively rational deal, no agent involved suffers a loss in utility and
at least one is better off. It may be noted that given the characterisation of
Definition 4 it is immediate that any cooperatively rational deal is perforce
also individually rational; the converse, however, clearly does not hold in general.
In some settings, an equitable deal may be neither cooperatively nor individually rational. One may
interpret such deals as one method of reducing inequality between the values agents
place on their allocations: for those involved in an equitable deal, it is
ensured that the agent who places least value on their current allocation will obtain
a resource set which is valued more highly. It may, of course, be the case that some agents
suffer a loss of utility: the condition for a deal to be equitable limits
how great such a loss could be. Finally the concept of Pigou-Dalton deal originates from and has
been studied in depth within the theory of exchange economies. This is one of many approaches
that have been proposed, again in order to describe deals which reduce inequality between
members of an agent society, e.g. [Endriss & Maudet, 2004b].
In terms of the definition given, such deals encapsulate the so-called
Pigou-Dalton principle in economic theory: that any transfer of income from a wealthy individual to
a poorer one should reduce the disparity between them.
We note that, in principle, we could define related rationality concepts based on
several extensions of this principle that have been suggested, e.g.
[Atkinson, 1970;
Chateauneuf et al., 2002;
Kolm, 1976]
Using the same  -contract path constructed in Theorem 3, we need only vary the
definitions of the utility functions employed in order to obtain,
-contract path constructed in Theorem 3, we need only vary the
definitions of the utility functions employed in order to obtain,
Proof. We employ exactly the same sequence of allocations  described in the proof of
Theorem 3 but modify the utility functions
described in the proof of
Theorem 3 but modify the utility functions
 for each case.
for each case.
- a.
- Choose
 with
with 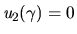 for all
for all
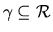 and
and
The resulting  -contract path is cooperatively rational: the utility enjoyed by
-contract path is cooperatively rational: the utility enjoyed by  remains constant
while that enjoyed by
remains constant
while that enjoyed by  increases by
increases by  with each deal. Any deviation from this
contract path (employing an alternative
with each deal. Any deviation from this
contract path (employing an alternative  -contract) will result in a loss of utility for
-contract) will result in a loss of utility for  .
.
- b.
- Choose
 with
with
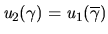 and
and
The  -contract path is equitable: both
-contract path is equitable: both  and
and  increase their respective utility values
by
increase their respective utility values
by  with each deal. Again, any
with each deal. Again, any  -contract deviating from this will result in both agents
losing some utility.
-contract deviating from this will result in both agents
losing some utility.
- c.
- Choose
 as
as
To see that the  -contract path consists of Pigou-Dalton deals, it suffices to
note that
-contract path consists of Pigou-Dalton deals, it suffices to
note that
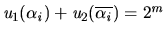 for each
for each  . In addition,
. In addition,
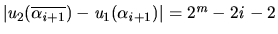 which is strictly less than
which is strictly less than
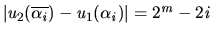 . Finally, any
. Finally, any  -contract
-contract
 which deviates from
this sequence will not be a Pigou-Dalton deal since
which deviates from
this sequence will not be a Pigou-Dalton deal since
which violates one of the conditions required of Pigou-Dalton deals.
The construction for two agent settings, easily extends to
larger numbers.
Corollary 2
For each of the choices of

considered in Theorem
3 and
Corollary
1, and all
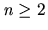
,
Proof. Fix allocations in which  is given
is given 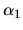 ,
,  allocated
allocated
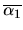 , and
, and  assigned
assigned
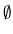 for each
for each 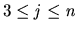 . Using identical utility functions
. Using identical utility functions
 as in each of the previous cases, we employ for
as in each of the previous cases, we employ for 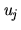 :
:
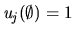 ,
, 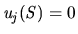 whenever
whenever
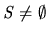 (
(
 as in Theorem 3);
as in Theorem 3);
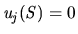 for all
for all  (Corollary 1(a));
(Corollary 1(a));
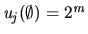 ,
, 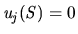 whenever
whenever
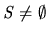 (Corollary 1(b)); and, finally,
(Corollary 1(b)); and, finally,
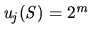 for all
for all  , (Corollary 1(c)). Considering a realisation
of the
, (Corollary 1(c)). Considering a realisation
of the  -deal
-deal
 the only
the only
 -contract path admissible is the path
-contract path admissible is the path  defined in the related proofs. This
gives the lower bound stated.
defined in the related proofs. This
gives the lower bound stated.
We note, at this point, some other consequences of Corollary 1 with respect to
[Endriss & Maudet, 2004b, Theorems 1, 3], which state
Fact 1
We recall that a

-path,

is
maximal if for each
allocation

,
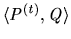
is
not a

-deal.
- a.
- If
 is any maximal path of cooperatively rational deals
then
is any maximal path of cooperatively rational deals
then 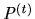 is Pareto optimal.
is Pareto optimal.
- b.
- If
 is any maximal path of equitable deals
then
is any maximal path of equitable deals
then 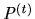 maximises the value
maximises the value
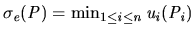 , i.e. the so-called
egalitarian social welfare.
, i.e. the so-called
egalitarian social welfare.
The sequence of cooperatively rational deals in Corollary 1(a) terminates
in the Pareto optimal allocation 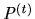 : the allocation for
: the allocation for  always
has utility
always
has utility  and there is no allocation to
and there is no allocation to  whose utility can exceed
whose utility can exceed  . Similarly,
the sequence of equitable deals in Corollary 1(b) terminates in the
allocation
. Similarly,
the sequence of equitable deals in Corollary 1(b) terminates in the
allocation 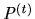 , for which
, for which
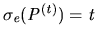 the maximum that can be attained for the instance defined. In both cases, however, the optima
are reached by sequences of exponentially many (in
the maximum that can be attained for the instance defined. In both cases, however, the optima
are reached by sequences of exponentially many (in  ) deals: thus, although Fact 1
guarantees convergence of particular deal sequences to optimal states it may be the
case, as illustrated in Corollary 1(a-b), that the process of convergence
takes considerable time.
) deals: thus, although Fact 1
guarantees convergence of particular deal sequences to optimal states it may be the
case, as illustrated in Corollary 1(a-b), that the process of convergence
takes considerable time.



Next: O-contract Paths - Monotone
Up: Lower Bounds on Path Length
Previous: Overview
Paul Dunne
2004-11-26
![]() in
in
![]() ,
with the following property4
,
with the following property4
![]() to be a longest such path with this property that could be formed
in
to be a longest such path with this property that could be formed
in
![]() , letting
, letting
![]() be the sequence of allocations
with
be the sequence of allocations
with
![]() .
We now define the utility functions
.
We now define the utility functions ![]() and
and ![]() so that for
so that for
![]() ,
,

![]() , i.e. a
sequence satisfying the condition (SC), is a lower bound on
, i.e. a
sequence satisfying the condition (SC), is a lower bound on
![]() .
These paths in
.
These paths in
![]() were originally
studied in [Kautz, 1958] in the context of coding theory and the lower bound
on their length of
were originally
studied in [Kautz, 1958] in the context of coding theory and the lower bound
on their length of ![]() established in [Abbott & Katchalski, 1991].
established in [Abbott & Katchalski, 1991].![]()
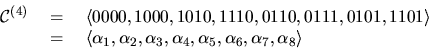
![]() -contract path constructed in Theorem 3, we need only vary the
definitions of the utility functions employed in order to obtain,
-contract path constructed in Theorem 3, we need only vary the
definitions of the utility functions employed in order to obtain,
![]() described in the proof of
Theorem 3 but modify the utility functions
described in the proof of
Theorem 3 but modify the utility functions
![]() for each case.
for each case.
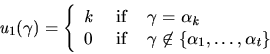
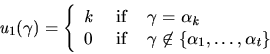
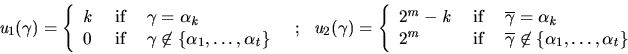
![]() is given
is given ![]() ,
, ![]() allocated
allocated
![]() , and
, and ![]() assigned
assigned
![]() for each
for each ![]() . Using identical utility functions
. Using identical utility functions
![]() as in each of the previous cases, we employ for
as in each of the previous cases, we employ for ![]() :
:
![]() ,
, ![]() whenever
whenever
![]() (
(
![]() as in Theorem 3);
as in Theorem 3);
![]() for all
for all ![]() (Corollary 1(a));
(Corollary 1(a));
![]() ,
, ![]() whenever
whenever
![]() (Corollary 1(b)); and, finally,
(Corollary 1(b)); and, finally,
![]() for all
for all ![]() , (Corollary 1(c)). Considering a realisation
of the
, (Corollary 1(c)). Considering a realisation
of the ![]() -deal
-deal
![]() the only
the only
![]() -contract path admissible is the path
-contract path admissible is the path ![]() defined in the related proofs. This
gives the lower bound stated.
defined in the related proofs. This
gives the lower bound stated.![]()