Experimental Results

**Table 4:** Performance statistics in Logistics Transportation Domain. Average solution length is shown in parentheses next to %Solved. Case retrieval time is shown in parentheses next to CPU time.
Phase		20	40	60	80	100	120
One Goal
%Solved	100%(3)	100%(3)	100%(3)	100%(3)	100%(3)	100%(3)	100%(3)
time(sec)	15	14(.1)	13(.1)	4(.0)	5(.10)	3(.13)	3(.13)
Two Goal
% Solved	90%(4)	93%(4)	100%(5)	100%(5)	100%(5)	100%(5)	100%(5)
time(sec)	1548	1069(.2)	22(1.0)	23(.2)	25(.28)	15(.28)	11(.26)
Three Goal
% Solved	53%(5)	87%(7)	93%(7)	93%(7)	93%(7)	100%(8)	100%(8)
time(sec)	7038	2214(.55)	1209(.49)	1203(.54)	1222(.52)	250(.54)	134(.58)
Four Goal
% Solved	43%(5)	100%(8)	100%(8)	100%(8)	100%(9)	100%(9)	100%(9)
time(sec)	8525	563(.99)	395(.79)	452(.91)	24(.97)	22(.89)	22(.88)
Five Goal
% Solved	0%	70%(11)	90%(11)	93%(11)	93%(11)	93%(11)	100%(12)
time(sec)	15000	5269(2)	2450(1)	1425(2)	1479(1)	1501(1)	375(1)
Six Goal
% Solved	0%	50%(12)	70%(13)	87%(14)	93%(14)	93%(14)	93%(14)
time(sec)	15000	7748(3)	4578(5)	2191(5)	1299(3)	1319(3)	1244(3)

**Figure 17:** Replay performance in the Logistics Transportation Domain with increasing amounts of training. Thirty problems were tested for each problem size (1 to 6 goals). The amount of time needed to solve all test problems up to that size (including case retrieval time) is shown when problems were solved from scratch (level 0) and with replay after increasing levels of training (after solving 20 ... 120 randomly generated problems). The insert shows the amount of time taken to solve all test problems after increasing amounts of training. A time limit of 500 seconds was placed on problem solving.
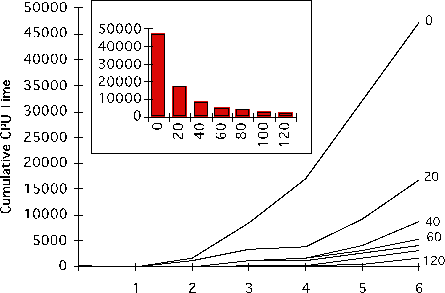
$\begin{figure} \centerline{ \epsfxsize=300pt \epsfbox{/ud/ai1/laurie/figs/JAIR-figure17.epsf}}\end{figure}$

**Figure 18:** Replay performance in the Logistics Transportation Domain scaled up to 15 cities. A case library was formed as 120 training problems (6 cities, 6 goals) were solved. This library was then used in solving test sets containing larger problems (15 cities, 6 to 10 goals). None of the problems were solved within the time limit (500 sec) in from-scratch mode. For replay mode, average solution length is shown in parentheses next to problem size.
$\begin{figure} \centerline{ \epsfxsize=300pt \epsfbox{/ud/ai1/laurie/figs/jair-figure18.epsf}}\end{figure}$

**Figure 19:** Replay performance in the logistics transportation. The percentage of test problems solved within the time limit (500 sec) is plotted against number of training problems solved. Percentage solved is shown for problems of increasing size (1, 3, and 5 goals).
$\begin{figure} \centerline{ \epsfxsize=250pt \epsfbox{/ud/ai1/laurie/figs/jair-figure19.epsf}}\end{figure}$

**Figure 20:** Figure shows the size of the case library with increased number of training problems solved. Library size increases with training problem size (1, 3, and 5 goals). 5' shows the number of single-goal subproblems contained in the 5-goal training problems.
$\begin{figure} \centerline{ \epsfxsize=250pt \epsfbox{/ud/ai1/laurie/figs/jair-figure20.epsf}}\end{figure}$

In the first experiment on the 6 city domain DERSNLP+EBL showed substantial improvements with multi-case replay as evident from the results in Table 4. Moreover, replay performance improved with problem-solving experience. The plans that were produced showed only a slight increase in number of steps over the solutions which were obtained in from-scratch mode. The same results are plotted in Figure 17 which graphs cumulative CPU time on all test problems over the six experiments. This figure illustrates how CPU time decreased with the number of training problems solved. The insert shows total CPU time (including case retrieval time) for all of the test problems in the six experiments. As evident in this insert, planning performance improves with increased experience on random problems. However, relatively little experience (20 problems solved) was enough to show significant performance improvements.

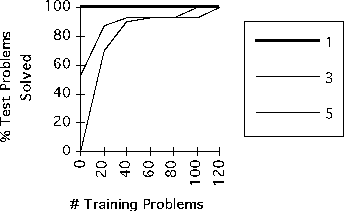
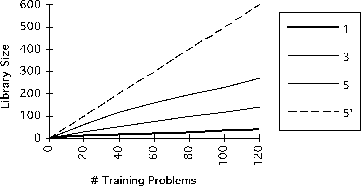
Replay raised the problem-solving horizon, as illustrated in Figure 19. It is more effective with larger problem size, when from-scratch planning tends to exceed the time limit imposed on problem-solving. Figure 20 shows the increase in the size of the library with increasing amounts of training. This figure also indicates that library size is determined more by the amount of interaction in the domain, as opposed to the number of training problems solved. The rate at which the case library grows tapers off and is higher when the planner is trained on larger problems.

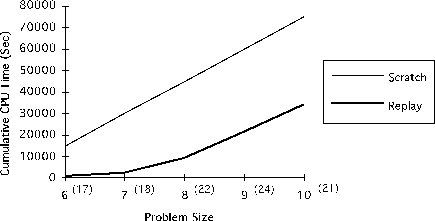
In the second experiment, a library formed over the course of training on 6-goal problems was used to solve larger problems (6 to 10 goals) in a more complex domain (15 cities) (See Figure 18). None of the larger problems were solved in from-scratch mode within the time limit of 500 sec . The planner continued to maximum time on all problems, indicated in the figure by the linear increase in CPU time. Its performance was substantially better with replay, however. Since library size was relatively small, the improvements in planning performance more than offset the cost of retrieving and adapting previous cases. This finding suggests that the replay strategy employed in these experiments represents an effective method for improving planning performance in complex domains.