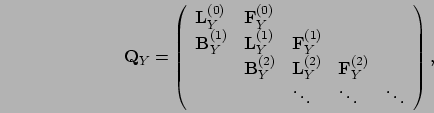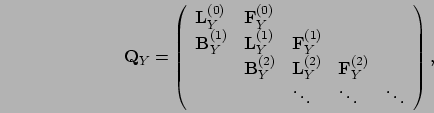Next: Definition of FB process
Up: Dimensionality reduction of Markov
Previous: Other approaches
Contents
FB, RFB, and GFB processes
In this section, we define the foreground-background (FB) process,
the recursive FB (RFB) process, and the generalized FB (GFB) process,
and provide examples of these processes.
In the rest of this chapter, we denote a matrix by a bold face letter such as
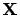 and its
and its 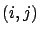 element by
element by
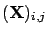 , and we
use
, and we
use 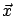 to denote a vector and
to denote a vector and 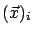 to denote its
to denote its
 -th element. Also, we use matrix
-th element. Also, we use matrix 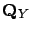 to denote the
generator matrix of a QBD process ``characterized by
parameter
to denote the
generator matrix of a QBD process ``characterized by
parameter  .'' Here,
.'' Here,  may be a single letter or number, denoting
process
may be a single letter or number, denoting
process  or the
or the  -th QBD process, or
-th QBD process, or  may be a pair of numbers
may be a pair of numbers
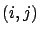 , denoting the
, denoting the  -th QBD process of type
-th QBD process of type  . Unless otherwise stated, we express
. Unless otherwise stated, we express
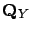 using submatrices,
using submatrices,
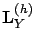 ,
,
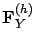 , and
, and
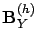 , such that
, such that
where
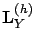 encodes (local) transitions within level
encodes (local) transitions within level  ,
,
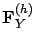 encodes (forward) transitions from level
encodes (forward) transitions from level  to level
to level
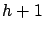 , and
, and
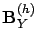 encodes (backward) transitions from level
encodes (backward) transitions from level  to
level
to
level 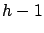 , for each
, for each  (see Section 3.2).
(see Section 3.2).
Subsections




Next: Definition of FB process
Up: Dimensionality reduction of Markov
Previous: Other approaches
Contents
Takayuki Osogami
2005-07-19