Proximity Queries between Convex Objects: An Interior Point Approach for Implicit Surfaces
 We develop an interior point approach to exact distance computation
between convex objects represented as intersections of implicit
surfaces. Exact distance computation algorithms are particularly
important for applications involving objects that make contact, such
as in multibody dynamic simulations and haptic interactions. In
contrast to geometric approaches developed for polyhedral objects, we
formulate the distance computation problem as a convex optimization
problem; this optimization formulation has been previously described
for polyhedral objects. Example implicit surfaces include planes
(polyhedra), quadrics, and generalizations of quadrics including
superquadrics and hyperquadrics, as well as intersections of these
surfaces.
We use an interior point method to solve the optimization problem and
demonstrate that for general convex objects represented as
implicit surfaces, interior point approaches are globally convergent,
and fast in practice. Further, they provide polynomial-time
guarantees for implicit surface objects when the implicit surfaces
have self-concordant barrier functions. We use a primal-dual interior
point algorithm that solves the KKT conditions obtained from the
convex programming formulation. For the case of polyhedra and
quadrics, we establish a theoretical time complexity of O(n^{1.5}),
where n is the number of constraints.
We present
implementation results for example implicit surface objects and
demonstrate that distance computation rates of about 1 kHz can be
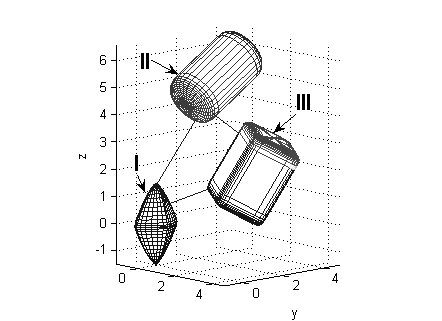
achieved. The figure on the right shows some example objects where
the line between two pairs is the line joining the closest points.
We develop an interior point approach to exact distance computation
between convex objects represented as intersections of implicit
surfaces. Exact distance computation algorithms are particularly
important for applications involving objects that make contact, such
as in multibody dynamic simulations and haptic interactions. In
contrast to geometric approaches developed for polyhedral objects, we
formulate the distance computation problem as a convex optimization
problem; this optimization formulation has been previously described
for polyhedral objects. Example implicit surfaces include planes
(polyhedra), quadrics, and generalizations of quadrics including
superquadrics and hyperquadrics, as well as intersections of these
surfaces.
We use an interior point method to solve the optimization problem and
demonstrate that for general convex objects represented as
implicit surfaces, interior point approaches are globally convergent,
and fast in practice. Further, they provide polynomial-time
guarantees for implicit surface objects when the implicit surfaces
have self-concordant barrier functions. We use a primal-dual interior
point algorithm that solves the KKT conditions obtained from the
convex programming formulation. For the case of polyhedra and
quadrics, we establish a theoretical time complexity of O(n^{1.5}),
where n is the number of constraints.
We present
implementation results for example implicit surface objects and
demonstrate that distance computation rates of about 1 kHz can be
achieved. The figure on the right shows some example objects where
the line between two pairs is the line joining the closest points.
- N. Chakraborty, J. Peng, S. Akella, and J. Mitchell, `` Proximity
Queries between Convex Objects: An Interior Point Approach for
Implicit Surfaces,'' IEEE Transactions on
Robotics , Vol. 24, No. 1,
pp. 211-220, February 2008.
- N. Chakraborty, J. Peng, J. Mitchell, and S. Akella, ``
Proximity Queries between
Convex Objects: An Interior Point Approach for Implicit Surfaces,'' 2006 IEEE International Conference on
Robotics and Automation , pp. 1910-1916, Orlando, FL, May 2006.
Dynamic Simulation of Multibody Systems with Intermittent Contact
- N. Chakraborty, S. Berard, S. Akella, and J. C. Trinkle, ``An Implicit Time-Stepping Method for Multibody Systems with Intermittent Contact'', Accepted. International Journal of Robotics Research, June 2013. [download]
-
N. Chakraborty, S. Berard, S. Akella, and J. C. Trinkle, ``
An Implicit
Time-Stepping Method for Quasi-Rigid Multibody Systems with
Intermittent Contact,'' Proceedings of ASME DETC'07 , Las Vegas, NV, September 2007.
- N. Chakraborty, S. Berard, S. Akella, and J. C. Trinkle,
``
An Implicit Time-Stepping Method for Multibody Systems with Intermittent Contact,''
Robotics: Science and Systems 2007,
Atlanta, GA, June 2007.
Recipient of Best Student Paper Award.
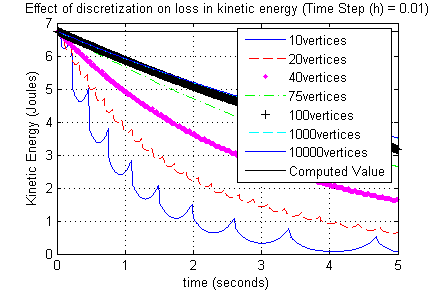
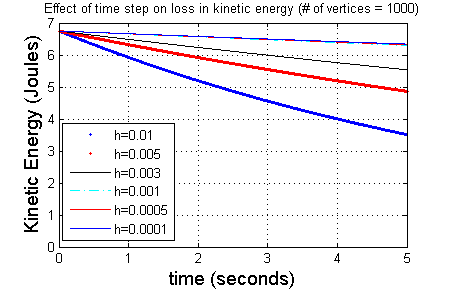
Two primary sources of stability and accuracy problems in time-stepping schemes for simulating multibody systems are the use of polyhedral representations of smooth bodies and the approximation of the distance function (arising from the decoupling of collision detection from the solution of the dynamic time-stepping subproblem). The effects of these common approximations can be seen using a simple example of a disc rolling without slip on a flat surface. The exact solution for this problem is: the disc will roll at constant speed ad infinitum. When the disc is approximated by a uniform regular polygon the figures above show: (a) For a given step size, the energy loss decreases as the number of edges increases, to a limit (left figure) (b) For a given number of edges, the energy loss decreases with decreasing step size, to a limit (right figure). Thus, using a discretized representation of the disc always results in a loss of energy, regardless of how small you set the step size or the number of edges used in the representation. In this work, we present an implicit time-stepping scheme for simulating multibody systems with intermittent contact by incorporating the contact constraints as a set of complementarity and algebraic equations within the dynamics model. We assume each object to be a convex object described by an intersection of convex inequalities. We write the contact constraints as complementarity constraints between the contact force and a distance function dependent on the closest points on the objects. The closest points satisfy a set of algebraic constraints obtained from the KKT conditions of the minimum distance problem. These algebraic equations and the complementarity constraints taken together ensure satisfaction of the contact constraints. This enables us to formulate a geometrically implicit time-stepping scheme (i.e., we do not need to approximate the distance function) as a nonlinear complementarity problem (NCP). The resulting time-stepper is therefore more accurate; further it is the first geometrically implicit time-stepper that does not rely on a closed form expression for the distance function. We first present our approach assuming the bodies to be rigid and then extend it to locally compliant or quasi-rigid bodies. We demonstrate through example simulations the fidelity of this approach to analytical solutions and previously described simulation results. In the left figure above the horizontal line (labeled computed value) is the result obtained using our proposed scheme (which clearly shows energy conservation within a numerical tolerance).
Use of dynamic simulation in motion planning
-
The (kinodynamic) motion planning problem can be thought of as inverse
of the dynamic simulation problem. In motion planning, given the
current state of the system and a goal state, we have to compute the
robot actuator inputs or forces such that the robot reaches its goal
state while satisfying geometric, kinematic, and dynamic constraints.
Sampling-based motion planning algorithms (e.g., Rapidly-exploring
Random Tree (RRT)) forms a discrete representation (graph-based) of
the state space incrementally. A key feature of existing
sampling-based motion planning algorithms is that during the formation
of the graph, a trajectory is first found that respects the dynamics
constraints (by integrating the equations of motion) and then the
trajectory is checked for collision. In cluttered environments,
because of the decoupling between dynamic time-stepping and collision
checking, finding a feasible input is difficult and sensitive to the
duration, Δt , of application of the input, and to the
discretization resolution of the input set. Thus, in cluttered
environments, finding a feasible trajectory and control input is hard
and computationally intensive.
Using a
motion model with collision avoidance constraints included within the
time stepper (as complementarity constraints) we can get the contact
forces when the robot contacts an object. Furthermore, since the
collision constraints are satisfied, the trajectory obtained is
feasible. This contact force can be transformed to the actuator space
(for fully actuated or redundantly actuated robots) to give an
actuator input that leads to a collision free path. Thus, use of a
complementarity-based dynamic simulation guarantees that one {\em
always gets a collision free trajectory and the corresponding
control inputs} during search. I proposed this novel use of the dynamic
time-steppers, which leads to algorithms that can solve motion planning
problems in cluttered environments that are difficult to solve with
current algorithms.
In this work, we present the use of complementarity-based dynamic
simulation algorithms for kinodynamic motion planning.
Dynamic simulation algorithms are used as local planning methods in
sampling-based motion planning algorithms to find inputs that ensure
the resulting trajectory satisfies the dynamics constraints. However,
the inputs are not guaranteed to give collision-free path segments.
The inputs, chosen either by random sampling or from a discretization
of the available inputs, are rejected if the path segment is not collision
free. In cluttered environments, finding a feasible input is difficult
and sensitive to the duration $\Delta t$ of application of the input,
and to the discretization resolution of the input set. When the
collision constraints (or any inequality constraints on the state of
the robot) are modeled as a set of complementarity constraints, the
dynamic simulation algorithm gives a path segment that touches the
obstacles and a set of {\em contact forces} whenever the robot makes
contact with the obstacles. The sum of the chosen input
forces and the contact forces transformed to the input space gives a
control input that guarantees a collision-free path segment (provided
it is within the actuator bounds). Thus in cluttered environments,
using a complementarity-based dynamic simulation algorithm, we can
find a feasible input that is relatively insensitive to the
choice of $\Delta t$ and the discretization resolution of the input
set. We present simple simulation examples showing the advantages of our
algorithm in cluttered environments.
-
N. Chakraborty, S. Akella, and J. C. Trinkle, ``
Complementarity-based Dynamic Simulation for Kinodynamic Motion Planning,'' 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems , St. Louis, MO, October 2009.
Back to top.
Back to Nilanjan's research interests