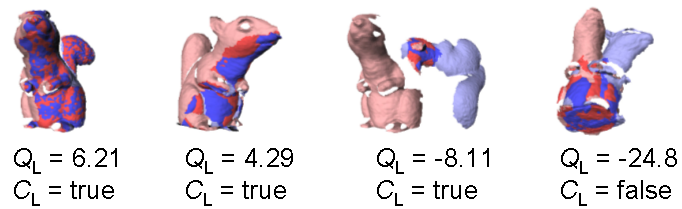A model hypothesis is a potential solution to our automatic modeling registration problem. Given a model hypothesis, we would like to know if it is a good quality solution or, more importantly, given two hypotheses, we would like to judge which one is better. However, model hypotheses are complex, so we start by looking at the quality of registration between a pair of views, which we call local quality. Later, we will see that we can extend this pair-wise quality measure to handle entire model hypotheses.

Maximum likelihood local quality model

The concept of local quality is related to the verification process present in most 3D object recognition systems. At some point, such a system must decide whether the hypothesized match is "good enough.'' Typically, this is done by thresholding some statistic of the data or of features derived from the data. The question is what statistic/features should be used and how to set the threshold. The answers depend on the sensor and the scene characteristics. For example, two surfaces that are ten centimeters apart might indicate a good registration for terrain observed from twenty meters away but not for a desktop object seen from one meter. Rather than relying on fixed, user-defined thresholds, which tend to be brittle, we explicitly model the behavior of the system for a given sensor and scene type, using supervised learning to determine a statistical model of local quality from training data. The benefit of this approach is that we do not need detailed knowledge of the sensor or even of the surface matching and pair-wise registration algorithms.

We have developed a statistical framework for representing local quality using Bayesian decision theory. We want to estimate the probability that a match is correct based on some measurements taken from the data - measurements such as the RMS distance between the surfaces in the overlapping regions, which we call overlap distance. We define the local quality (Q_L) as the log odds ratio of this probability. The probability distributions used to compute Q_L are learned from labeled training data using maximum likelihood parametric density estimation. The picture at right shows the probability distribution for overlap distance for a set of training pair-wise matches. As expected, correct matches tend to have smaller overlap distance than incorrect ones. The data for correct matches (M+) is shown in blue and the data for incorrect matches (M-) is shown in red. The maximum likelihood model for the data is shown in green and magenta.

With this probabilistic formulation, it is easy to combine several independent features into a single quality measure, since the probabilities are just multiplied. Moreover, disparate features with different units - such as color or texture similarity - can also be integrated using this framework. In the dissertation, we derive several local quality measures using this framework. The pictures below show several real pair-wise match results and their respective local quality measures. C_L is the output of a classifier that labels matches as correct or incorrect based on Q_L. Notice that the third example is an incorrect match but that the classifier labels it as correct. Such examples are the reason that we cannot solve the automatic modeling just by classifying pair-wise matches.

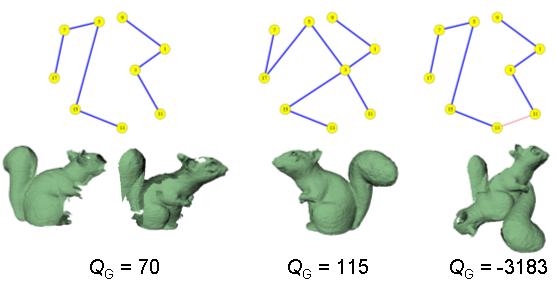
Extending to an entire model hypothesis

Assuming independence between the pair-wise matches, the quality of a model hypothesis can be computed simply by summing up the local quality measure for all pair-wise matches within the hypothesis. Rather than just using the adjacent views in a model hypothesis, however, we also include the indirectly connected views. For example, if view 1 is connected to view 2 and view 2 is connected to view 3, we check whether views 1 and 3 overlap and, if so, use that local quality as well. If all the pair-wise matches in a hypothesis are correct, these additional terms will serve as additional verification. If the hypothesis contains an incorrect match, then the chances are high that many of these additional terms will have low quality values, so the overall hypothesis will have a low quality value. We call the quality of a model hypothesis the global quality (Q_G). Below are some examples of global quality for different model hypotheses. The two part hypothesis on the left has a slightly lower quality than the single part hypothesis, while the incorrect hypothesis has an extremely low quality value.

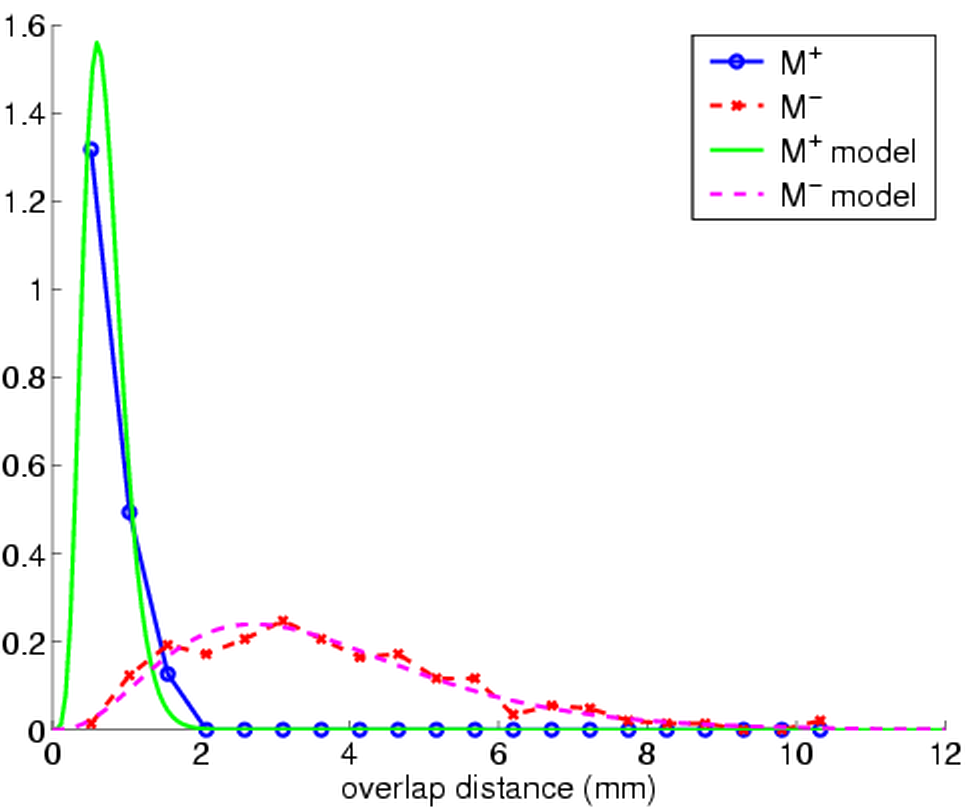Next: How do we find the best model hypothesis?