| Automatic 3D modeling from reality | |
|
How
do we find the best model hypothesis?
|
|
| Thesis Research |
Robotics Institute
|
| Daniel Huber |
Carnegie Mellon University
|
|
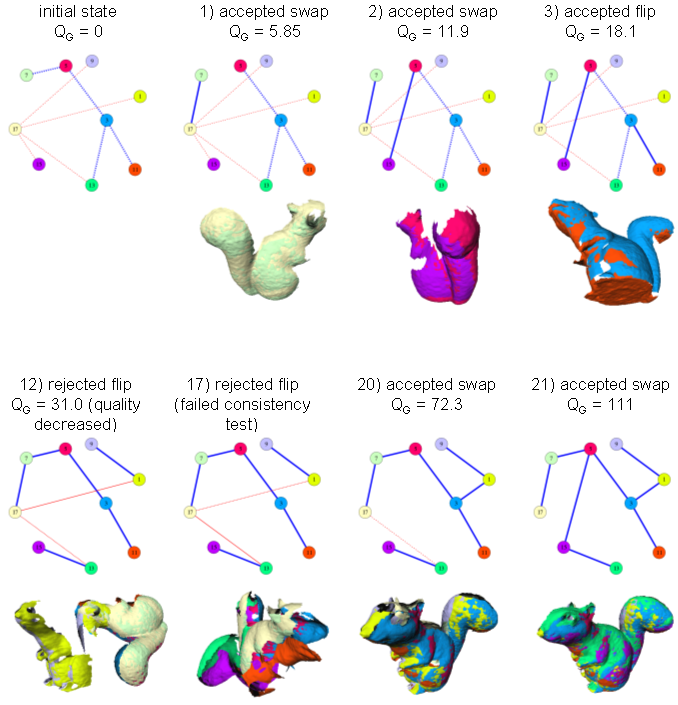
Assuming that we have a method for evaluating the quality of a given model hypothesis, the next question is "How do we find the best model hypothesis?" The problem is that the space of possible hypotheses is too large to search explicitly. Our approach is to use a stochastic algorithm to incrementally update an initial hypothesis, continually improving its quality until no better hypothesis can be found. Recall that a model hypothesis is a set of edges taken from the model graph of pair-wise registration results. The hypothesis is restricted to be a spanning tree of the model graph, and the edges have an attribute called visibility that breaks a model into two parts whenever an edge's visibility is set to hidden. Our algorithm begins with an initial hypothesis, which in our experiments is just a random model hypothesis with the visibility attribute of all edges set to hidden. Such a hypothesis is a multi-part model where each view is a separate part. We repeatedly update the current hypothesis using one of two update operations, an edge flip or an edge swap. An edge flip toggles the visibility state of a randomly chosen edge. Toggling from hidden to visible joins two sets of views in the model, while toggling from visible to hidden breaks the views apart. An edge swap involves removing a randomly chosen edge from the hypothesis and replacing it with another edge chosen at random from the model graph to re-establish the spanning tree requirement for the hypothesis.
The search algorithm repeatedly generates new hypotheses and evaluates their global quality. If the quality improves, the update is accepted, otherwise it is rejected. Some additional details and extensions are described in the dissertation. The pictures below show a trace of the algorithm in action (Note that it can be hard to see the dashed lines in the small picture. You can click on the image and see a larger version). Next: Results |
||||||||||||||